Just for Life.

明月更几时

0%

卷积神经网络

发表于 更新于
本文字数： 4.7k 阅读时长 ≈ 4 分钟

本文收录内容：

  • 边缘检测与卷积运算
  • 卷积神经网络的Keras实现
  • 残差网络，Inception，迁移学习的简单介绍。

重点是对于这些概念的理解，如果想观看具体概念的实现请往他处。

如果对本文有疑问或者想找男朋友，可以联系我，点击此处有我联系方式。

有关卷积

高通滤波器(HPF)是检测图像的某个区域，然后根据像素与周围像素的差值来提升该像素亮度的滤波器。以如下的核(kernal)为例，也称为滤波器(filter)。

1
2
3
[[0, -0.25, 0],
[-0.25, 1, -0.25],
[0, -0.25, 0]]

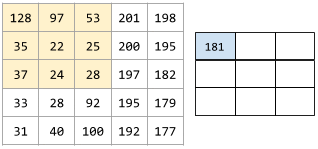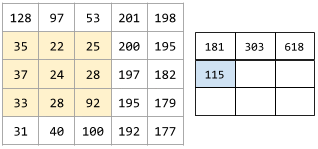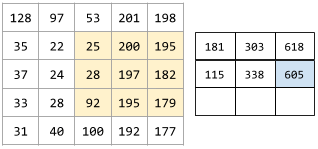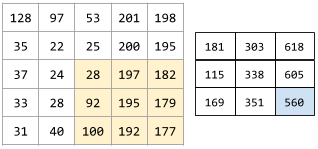
核是一组权重的集合，他会应用与原图像的一个区域，并生成目标区域的一个像素。可以将核视为一个窗口，这个窗口在原图像上移动时，覆盖区域的像素会按着某种形式(对应相乘相加)透过此窗口，形成一个像素点；随着窗口的不断移动，形成最终的目的图像(提取想要的特征)。如下所示。

卷积的过程中，原始图像尺寸会在滤波器的作用下会逐渐缩小，因此提供了两种卷积方式，一种是valid卷积(图像逐渐缩小)，一种是same卷积(图片大小不变)，Keras有对应函数。此外还有卷积步长，也就是filter一次移动的长度，和滤波器的大小共同决定了原始图像会缩小多少。

实战一下，在设置核后，与读入的图像进行卷积运算，卷积运算可以使用opencv提供的函数实现。

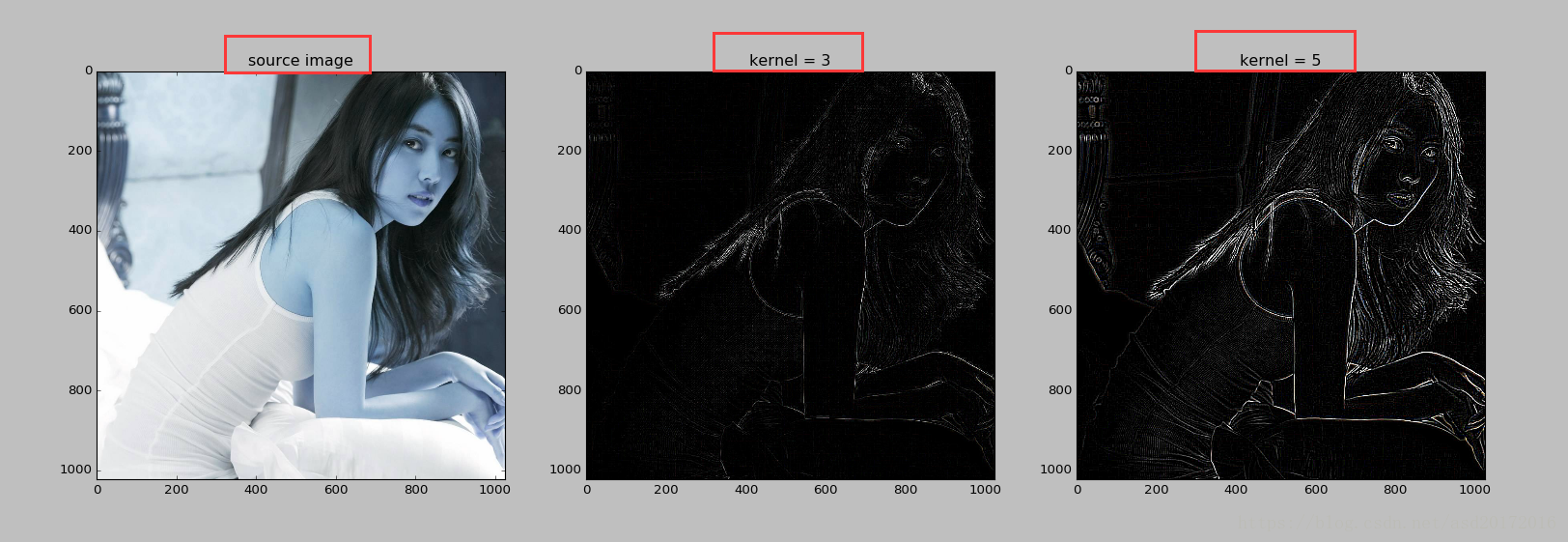
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import cv2
import numpy as np
import matplotlib.pyplot as plt

kernel_9 = np.array([[-1, -1, -1],
                     [-1, 8, -1],
                     [-1, -1, -1]])

kernel_25 = np.array([[-1, -1, -1, -1, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, 2, 4, 2, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, -1, -1, -1, -1]])

img = cv2.imread('test.jpg')
ndimg = np.array(img)

k3 = cv2.filter2D(ndimg, -1, kernel_9)      #convolve calculate 
k5 = cv2.filter2D(ndimg, -1, kernel_25)     #the second parameters measns the deepth of passageway.
#such as cv2.CV_8U means every passageway is 8 bit.
#-1 means the passageway of the source file and the object file is equal.
plt.subplot(131)
plt.imshow(img)
plt.title("source image")

plt.subplot(132)
plt.imshow(k3)
plt.title("kernel = 3")

plt.subplot(133)
plt.imshow(k5)
plt.title("kernel = 5")

plt.show()

得到的结果如下：

与高通滤波器相反的还有低通滤波器(LPF)，低筒滤波器与高通滤波器相反，当一个像素与周围像素的插值小于一个特定值时，平滑该像素的亮度，用于去燥和模糊化，比如PS软件中的高斯模糊，就是常见的模糊滤波器之一，属于削弱高频信号的低通滤波器。

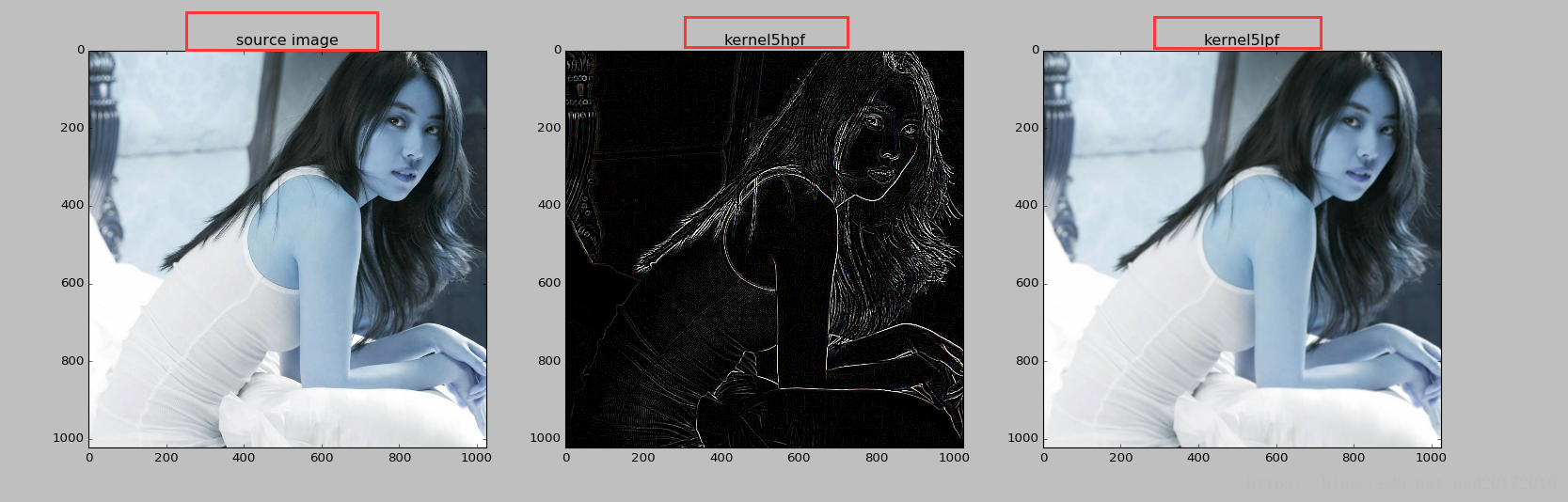
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import cv2
import numpy as np
import matplotlib.pyplot as plt

kernel_25h = np.array([[-1, -1, -1, -1, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, 2, 4, 2, -1],
                      [-1, 1, 2, 1, -1],
                      [-1, -1, -1, -1, -1]])

kernel_25l = np.array([[0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04],
                      [0.04, 0.04, 0.04, 0.04, 0.04]])

img = cv2.imread('test.jpg')
ndimg = np.array(img)

k3 = cv2.filter2D(ndimg, -1, kernel_25h)
k5 = cv2.filter2D(ndimg, -1, kernel_25l)

plt.subplot(131)
plt.imshow(img)
plt.title("source image")

plt.subplot(132)
plt.imshow(k3)
plt.title("kernel5hpf")

plt.subplot(133)
plt.imshow(k5)
plt.title("kernel5lpf")
plt.show()

结果如下：中间的图为高通滤波，最右方的图为模糊化后的。

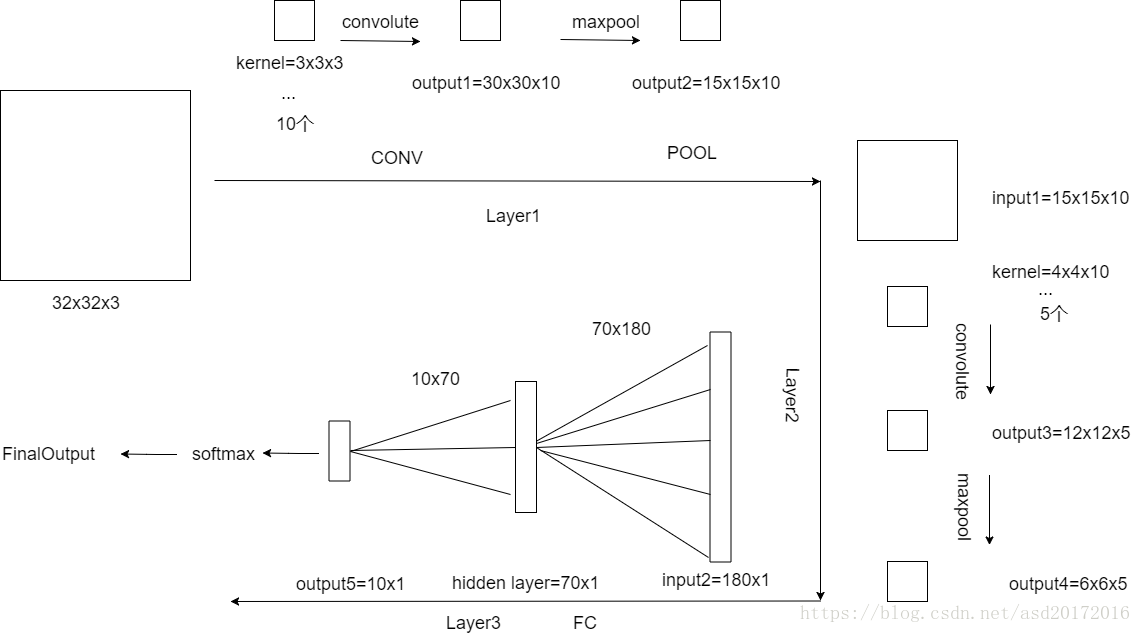
有关卷积神经网络

在下图中，伴随着三个卷积核对原始图像进行卷积，每个卷积核加一个偏执项biases，这一层网络便会得到三维的输出结果，即输出的通道数(channels)等于检测的特征数(filter numbers)，可以认为一个滤波器检测一个特征。

对比全连接神经网络，卷积的优点显而易见：参数共享(每次的输入图像都公用滤波器)、稀疏连接(滤波器的参数明显少于全连接网络的参数数量)。

卷积过后一般会伴随池化，池化虽然没有参数可以调节，但是最大池化会保留下区域的最大的特征(平均池化会淡化最强烈的特征)，最强烈的特征也更加易于区分，使得神经网络的工作更有效。

至此，无论是LeNet，Alexnet，VGG16这些经典的网络的共性便是卷积、池化、卷积、池化一层层堆叠，最后全连接至softmax进行判别分类。

使用Keras搭建卷积神经网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D

# Generate dummy data
x_train = np.random.random((100, 32, 32, 3))
y_train = keras.utils.to_categorical(np.random.randint(10, size=(100, 1)), num_classes=10)
x_test = np.random.random((20, 32, 32, 3))
y_test = keras.utils.to_categorical(np.random.randint(10, size=(20, 1)), num_classes=10)

model = Sequential()
# input: 32x32 images with 3 channels -> (32, 32, 3) tensors.
# this applies 32 convolution filters of size 3x3 each.
model.add(Conv2D(10, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))

model.add(Conv2D(5, (4, 4), activation='relu', input_shape=(15, 15, 10)))
model.add(MaxPooling2D(pool_size=(2, 2)))

model.add(Flatten())
model.add(Dense(180, activation='relu'))
model.add(Dense(70, activation='relu'))
model.add(Dense(10, activation='softmax'))

from keras.optimizers import SGD

sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='categorical_crossentropy', optimizer=sgd)

model.fit(x_train, y_train, batch_size=32, epochs=10)
score = model.evaluate(x_test, y_test, batch_size=32)

残差网络ResNets

在传统的网络中，数据的传播都是由上一层到下一层，下一层再到下下层，是一种顺序传播的形式。

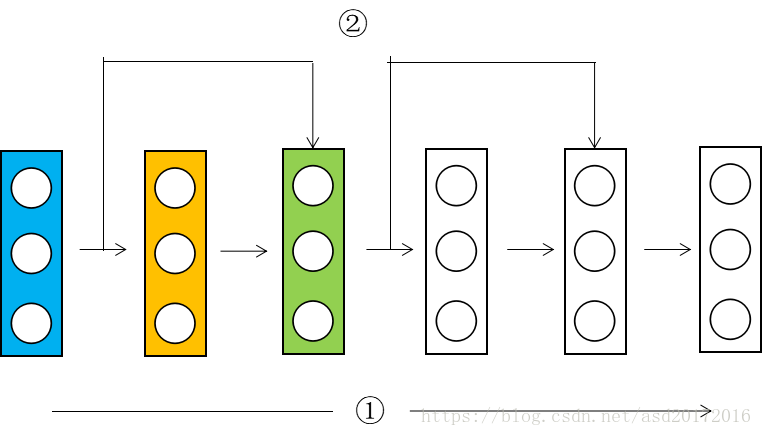
那么能不能从第一层直接传递到第十层，或者最后一层呢？这就是跳远连接的形式，第一层跨过好几层直接连接到后面的网络，如下图所示。

在上图中，蓝色的层输出的数据记为$X$，只考虑一号线，沿着一号线向绿色的层传播时，黄色层的输入为$X_1$，输出为$g(W_1X+b_1)$，记为$Z_1$。绿色层的输入为$Z_1$，输出记为$Z_2$。再来看上面的二号线，就是跳远连接的形式。考虑到二号线时，绿色层的输入是什么呢，是$Z_1+X_1$，即黄色层的输出加上最初的输入作为绿色层的输入。绿色层的输出是对输入的激活。上面的黄色层和绿色层就组成了一个残差块；二号线的连接形式即为跳远连接。

继续以上的内容，假设给一个神经网络添加两层，也就是一个残差块，做一个极端的假设，我们用了relu激活函数，残差块的输入$X_1$(正数)和残差块的输出(正数)保持一致，也就是$g(W_2X_2+b_2+X_1)=X_1$，可以推出$W_2=0,b_2=0$，让一个神经网络去学习这样的一个恒等式不是什么难度。

在跳远连接的过程中，增加这两层和不增加这两层的区别是一样的，也就是，现在我们可以增加网络的层数了。当然也不可能完美的学习出这样的恒等式，如果在学习恒等式的过程中学到了一些其他的有用信息，会提升学习的效率，毕竟恒等式只能保证效率而不是提升效率，可能这就是残差网络的神奇之处。

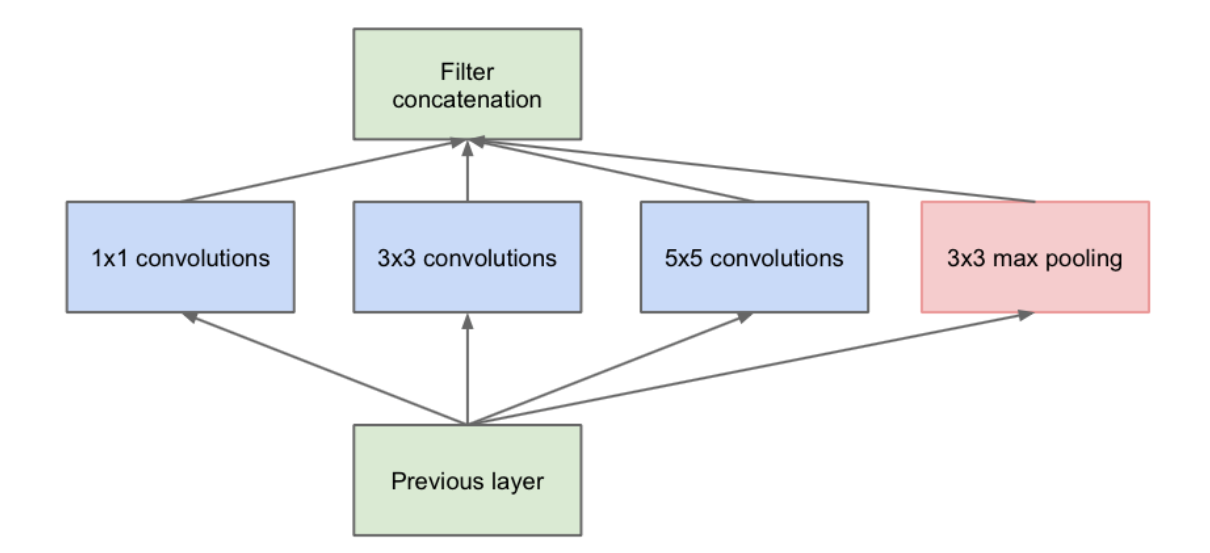
Inception 网络

与上述经典网络不同的是，Inceotion网络使用了1 $\times$ 1的filter，将多个特征求和便得到了二维的输出，1个这样的滤波器将维度压缩到二维，那么多个1 $\times$ 1 的filter便实现了对上一层输出channels的约减，降低数据维度。

如上图所示，对前一层进行不同的卷积运算(same)后会有多个输出(不同滤波器看到的特征也不同)，将这些输出的结果和池化运算堆叠在一起，得到了这一层的输出，并且作为下一层的输入。不同的卷积结果堆叠在一起使得特征具有更深的维度，多个这样的模块堆叠在一起使得网络更深。

残差网络，inception暂时没有实现代码，等到哪天参加破比赛需要这些的时候在补上吧。暂时没写这个代码的经验，写出来也无非是Ctrl C和Ctrl V，没有灵魂。

本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章