循环神经网络

趁寒假看完了DeepLearning的前生今世之后，用了一个下午自己推导了一番，想来还是留下个电子版的整理，供他人交流和日后查阅。（其实是我纸质版整理的太丑了）。

本文收录内容：

循环神经网络的基本概念
循环网络的经典结构
LSTM与GRU的keras实现，自行查阅keras文档喽

重点是对于这些概念的理解，尽力写下人能看懂的公式描述，知道在什么背景下调用和背后的数学观念就可以啦。

背景

在NLP开车，语音识别，视频处理，机器翻译等领域，和面临着一段连续的输入，这个输入的前后还有关系，比如机器翻译时：

The cats are full then sleeping on the tree.

我英语比较差，这句话的意思是一群猫吃饱了在树上睡觉，用are的原因是前面是cats复数，so，像这样序列化的输入，前后有关系的样本数据，通常会采用循环神经网络进行训练。

如果这类输入采用普通的全连接神经网络的话，每个句子长短不一，第一层神经元的数量怎么定义是不是？

萌新阶段

建立一个网络来判断一个单词是不是人名，这个技术在搜索引擎中会被用到。

当然为什么不采用查词典的技术呢？比如用查字典的方法也能解决，学过数据结构的话，知道这种情况建立索引查询会更快。如果一个人的名字是White(怀特)，总不能翻译成白色吧，判断是否是人名还得根据语境。

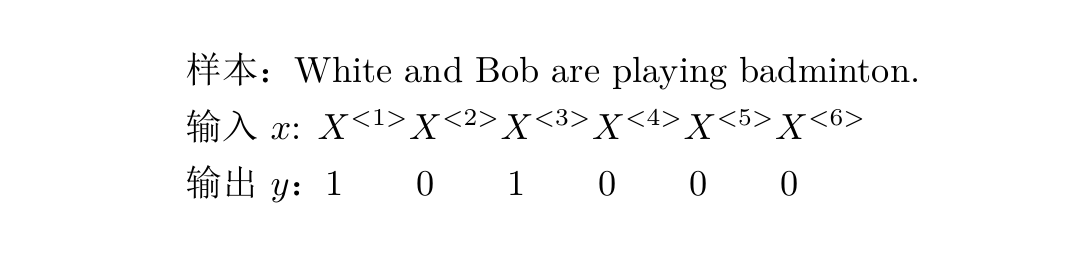
如上图所示，一个单词是一个输入，一句话是一个样本，1表示为人名，0表示不是。那么构建个什么样子的网络进行训练呢？而且还得解决每个样本输入维度不统一的问题。网络结构如下：

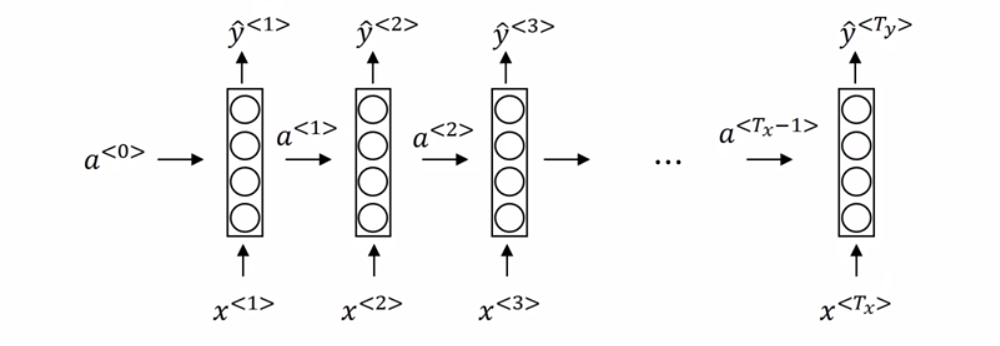
然后来解释下网络是如何运行的，参数的含义：

首先，$T_x$表示一个样本中单词的数量，$\hat{y}^{<1>}$表示对样本中第一个单词的预测，$a$就是个中间变量，图上画得一个方框加四个圈表示计算过程。$X^{<1>}$会经过one-hot编码处理，假设样本数据库共有10000个单词，$X^{<1>}$为第一个单词，假设在词典排序中的位置为7893，那么$X^{<1>}$就是一个长度为10000，只有第7893个位置是1的零向量，其余单词也是经过one-hot处理数值化。Keras中使用序列模型进行分类时，通常都会对类别进行one-hot编码：

1 2	import keras y_labels = keras.utils.to_categorical(y_label, num_classes=10)

$a^{<0>}$是个初始化的零向量，推算$a^{<1>}$和$\hat{y}^{<1>}$的方式为：
\begin{equation}
a^{<1>}=g(W_{aa}a^{<0>}+W_{ax}X^{<1>}+b_a)
\end{equation}
$g$表示某种激活函数如RELU，$W_{aa}$为和$a$相乘的参数，$W_{ax}$表示和样本输入相乘的参数。输出的$a^{<1>}$为下一层的输入。
\begin{equation}
\hat{y}^{<1>}=f(W_{ya}a^{<1>}+b_y)
\end{equation}
$f$表示某种激活函数如RELU，$W_{ya}$为另外的和$a$相乘的参数。此外，在循环神经网络中参数是共享的以减少计算复杂度，对于之后每个输入的单词，$W_{ya},W_{ax},W_{aa}$都是一样的。

推广到一般形式，第$t$个输入的单词(第$t$个时间步)的计算为：

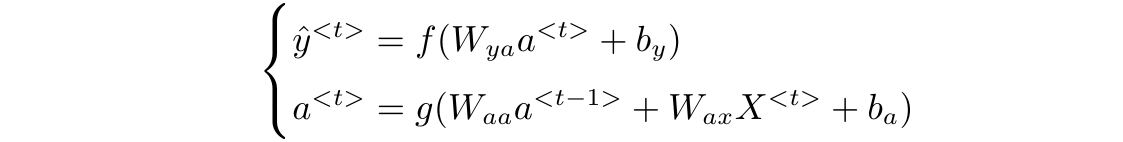
这样，有几个单词就有几个$X$，这个网络就走几次，输入结束的话也就停止。在训练时，方向传播成本函数$y$与$\hat{y}$的交叉熵来梯度下降，最终达到预测的目标。

推广结构

也许会好奇，在机器翻译时，输入与输出的数量是不相等的呀，处理影评的时候，多个单词的输入只会变成一个评分，这个时候就需要对网络的结构进行略微的修改。

影评：多个输入对应一个输出

音乐合成：一个输入对应多个输出

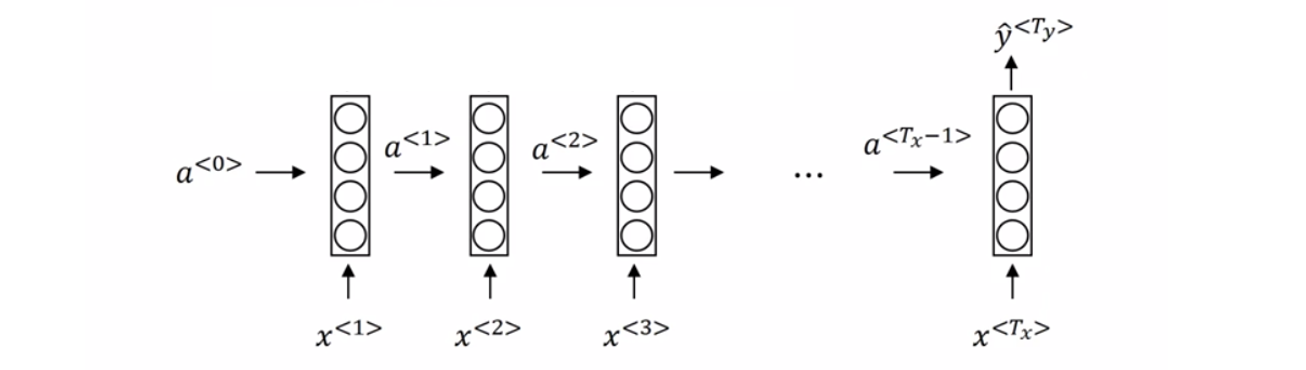
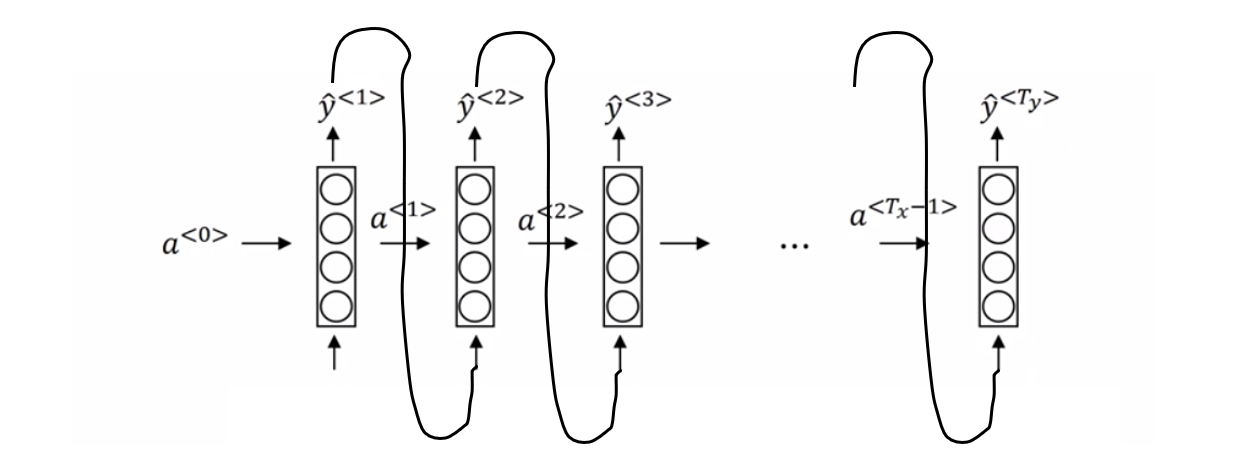
此时第一次的输出作为下一次的输入使用，利用上一次的信息推理下一次的信息，更加连贯。

机器翻译：输入与输出不同

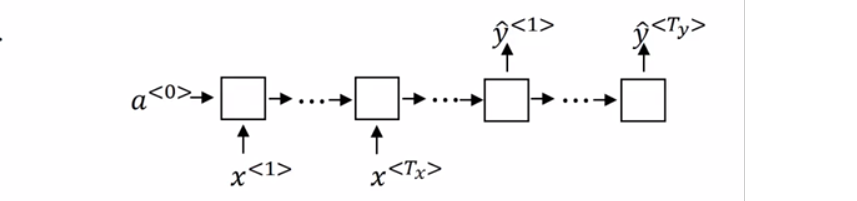
其中$x$的部分称为编码器，将单词编码为数字，$y$为解码器，将数字预测为单词。这个图也可以作为生成模型的范例，以一个训练好的问答模型为例：当只有几个词作为输入时，可以预测之后最有可能输出的单词。比如简单的问答模型，输入：Mountain height is，那么能够计算出mountain height is 后面最有可能出现的几个单词，直到预测出句子结束的标志。这样就可以判断出山的高度是多少，一个简单的人工智障系统就出来了。

RNN的信息利用

来一个很长很长的句子为例：

The cats, which eat fish, fruit and vegetables brought store are full then sleeping on the tree.

意思是，一群猫吃了从商店买来的鱼，水果和蔬菜后，吃饱了在树上睡觉，cats 和 are 之间间隔了很多单词，对于普通的RNN而言，很难记忆如此长的信息，专业一点就是后面学习到的梯度反向传播到前面就没了，前面的单词是复数，后面应该用are。这个时候LSTM和GRU便登上了历史舞台。

GRU

GRU称为门控循环单元，即在网络中设立一个门，确保神经网络在输入长文本信息后能够记忆前面的单词是复数还是单数。

取消前面的网络中间生成的变量$a$，这里暂时用$c$记忆细胞代替。来看一下GRU的门控结构：

此时$c$的计算方式为：

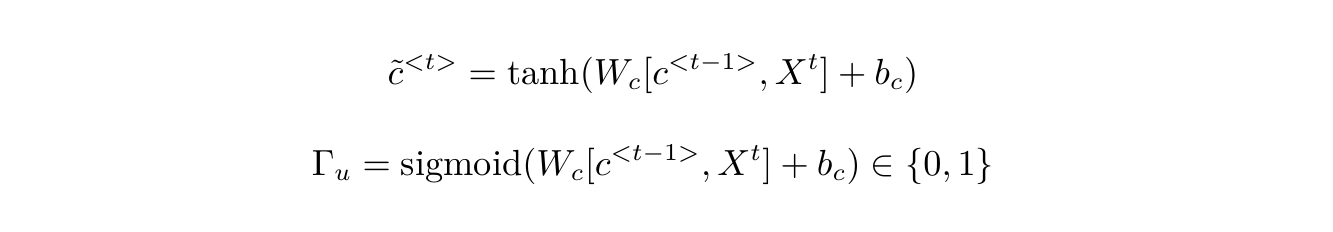
使用$\tilde{c}$来更新$c$，而是否更新则取决于记忆门$\Gamma_u$，当$\Gamma_u$为1时，更新信息，为0时取消更新。如果$\Gamma_u$一直不更新，$c$就会长时间记忆之前的信息，保持了长时间的记忆，避免了梯度消失。

推广到一般形式，$c$的计算形式和GRU的预测方法为：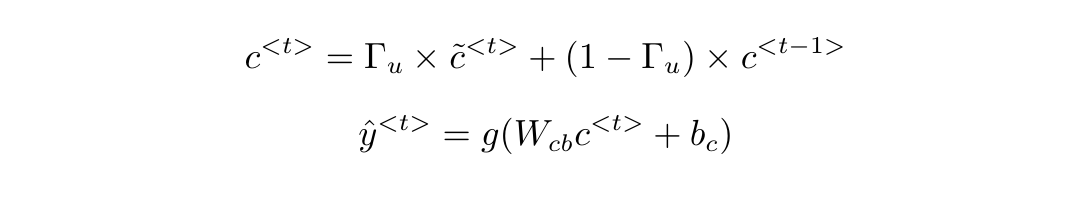

泛化为LSTM

LSTM与GRU大同小异，在GRU记忆门的基础上添加了遗忘门$\Gamma_f$，公式如下：

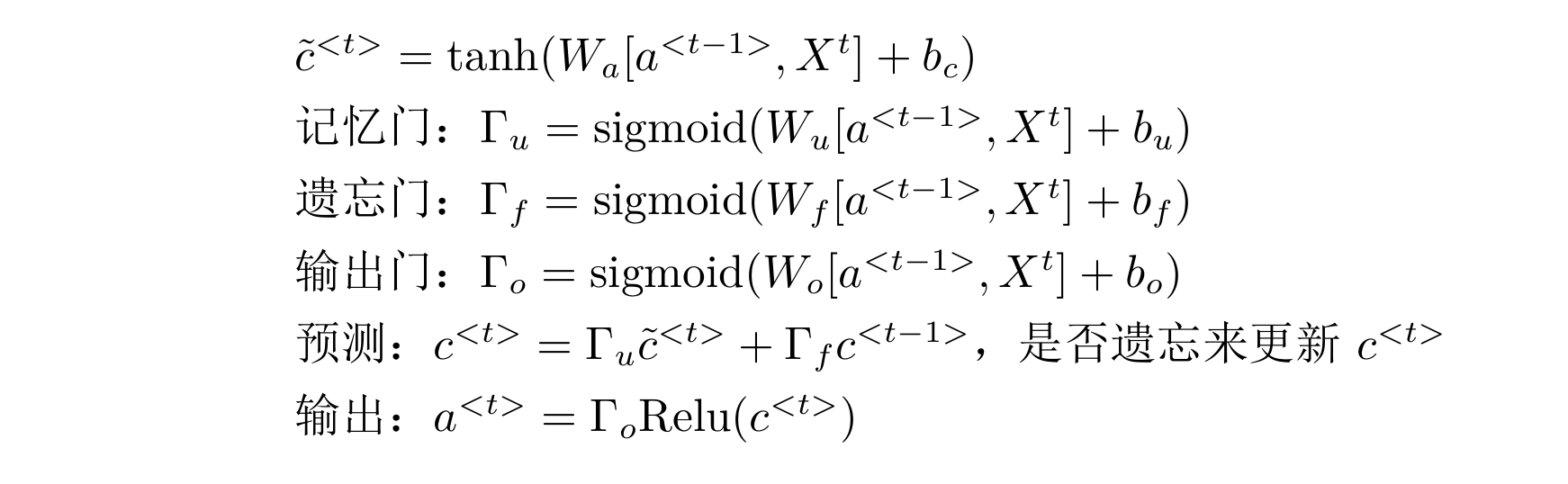
$\hat{y}$的计算和以前一样，使用了遗忘门$\Gamma_f$来代替之前的$1-\Gamma_u$，也就是，GRU实际是复杂的LSTM的简化版本。实际上，LSTM有更强健的结构，也更加强大和善于记忆，缺陷就是不易计算。

一个极度简单的LSTM实现：

import numpy as np
import keras

# Generate dummy data
x_train = np.random.random((1000, 20))
y_train = keras.utils.to_categorical(np.random.randint(10, size=(1000, 1)), num_classes=10)

from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import LSTM

max_features = 20

model = Sequential()
# 嵌入层
model.add(Embedding(max_features, output_dim=256))
model.add(LSTM(128))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))

model.compile(loss='binary_crossentropy',
              optimizer='rmsprop',
              metrics=['accuracy'])

model.fit(x_train, y_train, batch_size=16, epochs=10)

偷窥孔连接

就是在LSTM中的三个门，记忆门、遗忘门、输出门的$W$乘的矩阵中$a,b$中在加入$t-1$时刻的$c$，也就是考虑了$t-1$时刻的记忆情况和输出情况，猜想他们共同影响了$t$时刻三个门的状况。(个人感觉多此一举)。