Just for Life.

明月更几时

0%

正则化与标准化

发表于 更新于
本文字数： 10k 阅读时长 ≈ 9 分钟

来整理一下在机器学习中常用的优化方法，无非是在容易出问题的地方加入人的调控，包括数据数据，数据处理，反向传播，梯度函数等方面，在各种容易出问题的地方加入调控，使得神经网络更有效，或者说神经网络的运行在你的控制之中，而不是调了一堆参数后网络没有优化，甚至调一些无关紧要的参数。

本文收录内容：

  • 正则化的常用方式与实现
  • 有关数据输入和传输的处理
  • 优化后的梯度函数

还是在实际的背景下对于这些概念的理解，学会变通和利用已有的知识进行问题转换。

正则化

正则化主要有 $L_1$ 和 $L_2$ 正则化，主要是针对参数 $w$ 的约束，因为这个参数决定了拟合曲线的形状，而偏执 $b$ 表示了偏移量。正则化是为了避免模型过拟合，或者说，能避免过拟合的都是正则化。我们以 $p$ 范数作为约束进行正则化，写出一般形式：

\begin{equation}
\begin{aligned}
{ } &\min L(\theta; x) \\
{ } &s.t. ||w||_p -C \leq 0
\end{aligned}
\end{equation}

那么上述不等式就是限制 $w$ 到原点的 $p$ 范数距离小于等于 $C$，那么将约束转换为拉格朗日乘数表现为：

\begin{equation}
\begin{aligned}
{ } &\min L(\theta; x) + \lambda (||w||_p - C)\\
{ } &\min _w \max_\lambda (w, \lambda)\\
{ } &s.t. \lambda \geq 0
\end{aligned}
\end{equation}

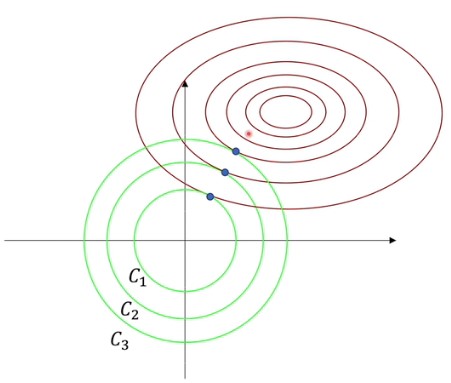
如上图所示，假设 $w$ 向量里只有两个参数，因此对应了这两个轴。绿色的使可行域范围，圈是损失函数等高线。在可行域范围，根据拉格朗日乘数的公式，我们知道相交处存在相反的梯度，即目标方程梯度为零，也就是约束范围内的极值点。而 $L_1$ 或 $L_2$ 正则化的约束为凸集，因此存在最优解。

再把拉格朗日乘数方程转化一下，我们可以得到以下结论：

\begin{equation}
\begin{aligned}
{ } &\min L(\theta; x) + \lambda (||w||_p - C)\\
{ } & \Rightarrow L(w) + \lambda ||w||_p
\end{aligned}
\end{equation}

虽然这两个方程的最值不一样，但取得最值时，$w$ 是一样的。那么上图中参数 $C$ 决定的是半径，在经过等价变形后，可以任意半径的圆，对应不同的极值点。

L2正则化

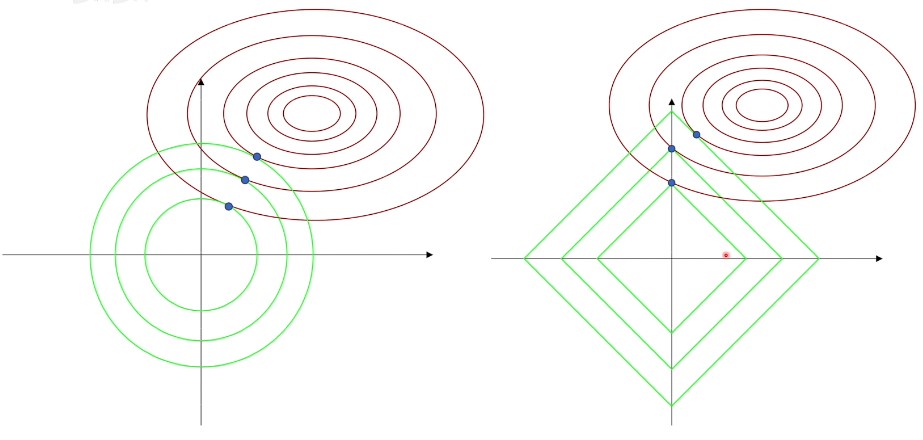
上图中，右侧是 $L_1$ 正则化在坐标轴，可以看到大部分即指点在坐标轴上，这就导致了部分特征的权重为 0，即一些特征被忽略，带来了稀疏性，仅仅是单个特征起作用，而去除特征的耦合避免过拟合。$L_2$ 则是通过减少权重的绝对值来避免过拟合。

假设此时的成本函数为：

那么在这个成本函数的后面加入正则项，修改之前的成本函数为：

$\lambda$是需要自己调节的正则化参数，因为对于网络的参数而言，$w$比$b$要多得多，而且影响在非线性空间内，对于线性空间的调节较为容易，所以正则项中是不含有$b$的。

L2正则化为何有效

这个正则项是如何工作的呢？在反向传播时，利用代价函数对$l$层的$w$进行梯度下降，得到：

  • 于是在参数$w$更新的过程中，会减去额外的正则项，也就是相对于正常的反向传播多了一个衰减的过程，衰减到合适的范围内。假设当$\lambda$足够大时，会有许多的$w$会近似为零，导致正向传播时输出$z$也位于0的附近。两点好处：$w$近似为0会缩小了网络的规模，防止了过拟合。

  • 输出$z$近似0会使得$z$位于激活函数最容易激活的区域，比如$\mathrm{sigmoid}$函数在$x=0$处的导数最大，利于网络的学习。

  • 逐渐减少高次项，避免过拟合。在高数中学过，损失函数在某个 $w$ 处展开，如果展开 $n$ 项，那么此时的曲线越复杂，也就是越过拟合，如果要减少曲线的复杂程度，就要减少泰勒展开后高次项的系数，也就是参数 $w$。而且观察更新时的正则梯度，对于数值越大的$w$，参数下降的幅度也就越大。

简单的Tensorflow实现

这里创建了一个差不多的模型，一个小规模网络，一个大规模网络，还有一个正则化的网络，进行对比，了解正则项的作用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
import tensorflow as tf
from tensorflow import keras

import numpy as np
import matplotlib.pyplot as plt

NUM_WORDS = 10000

(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)

# data preprocessing
def multi_hot_sequences(sequences, dimension):
    # Create an all-zero matrix of shape (len(sequences), dimension)
    results = np.zeros((len(sequences), dimension))
    for i, word_indices in enumerate(sequences):
        results[i, word_indices] = 1.0  # set specific indices of results[i] to 1s
    return results

train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)

# basic model
baseline_model = keras.Sequential([
    # `input_shape` is only required here so that `.summary` works.
    keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dense(16, activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

baseline_model.compile(optimizer='adam',
                       loss='binary_crossentropy',
                       metrics=['accuracy', 'binary_crossentropy'])

baseline_history = baseline_model.fit(train_data,
                                      train_labels,
                                      epochs=20,
                                      batch_size=512,
                                      validation_data=(test_data, test_labels),
                                      verbose=2)

# smaller model
smaller_model = keras.Sequential([
    keras.layers.Dense(4, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dense(4, activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

smaller_model.compile(optimizer='adam',
                loss='binary_crossentropy',
                metrics=['accuracy', 'binary_crossentropy'])

smaller_history = smaller_model.fit(train_data,
                                    train_labels,
                                    epochs=20,
                                    batch_size=512,
                                    validation_data=(test_data, test_labels),
                                    verbose=2)

# bigger model
bigger_model = keras.models.Sequential([
    keras.layers.Dense(512, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dense(512, activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

bigger_model.compile(optimizer='adam',
                     loss='binary_crossentropy',
                     metrics=['accuracy','binary_crossentropy'])

bigger_history = bigger_model.fit(train_data, train_labels,
                                  epochs=20,
                                  batch_size=512,
                                  validation_data=(test_data, test_labels),
                                  verbose=2)

# 对比效果
def plot_history(histories, key='binary_crossentropy'):
    plt.figure(figsize=(16,10))
    for name, history in histories:
        val = plt.plot(history.epoch, history.history['val_'+key],
                   '--', label=name.title()+' Val')
        plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
             label=name.title()+' Train')

    plt.xlabel('Epochs')
    plt.ylabel(key.replace('_',' ').title())
    plt.legend()

    plt.xlim([0,max(history.epoch)])

plot_history([('baseline', baseline_history),
              ('smaller', smaller_history),
              ('bigger', bigger_history)])

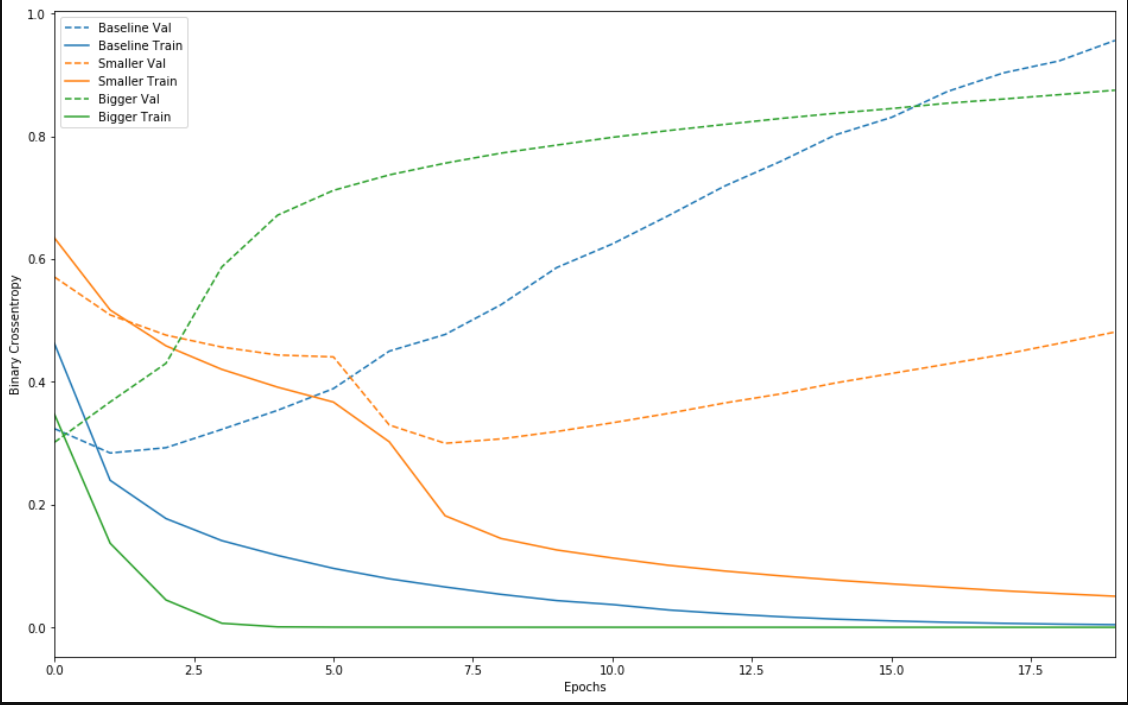
发现效果是这样的，较大的网络几乎仅仅1个周期之后便立即开始过拟合，并且之后严重多。网络容量越大，便能够越快对训练数据进行建模（产生较低的训练损失），但越容易过拟合（导致训练损失与验证损失之间的差异很大）。

奥卡姆剃刀定律：如果对于同一现象有两种解释，最可能正确的解释是“最简单”的解释，即做出最少量假设的解释。这也适用于神经网络学习的模型：给定一些训练数据和一个网络架构，有多组权重值（多个模型）可以解释数据，而简单模型比复杂模型更不容易过拟合。

加入正则的效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
l2_model = keras.models.Sequential([
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
                       activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
                       activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

l2_model.compile(optimizer='adam',
                 loss='binary_crossentropy',
                 metrics=['accuracy', 'binary_crossentropy'])

l2_model_history = l2_model.fit(train_data, train_labels,
                                epochs=20,
                                batch_size=512,
                                validation_data=(test_data, test_labels),
                                verbose=2)

plot_history([('baseline', baseline_history),
              ('l2', l2_model_history)])

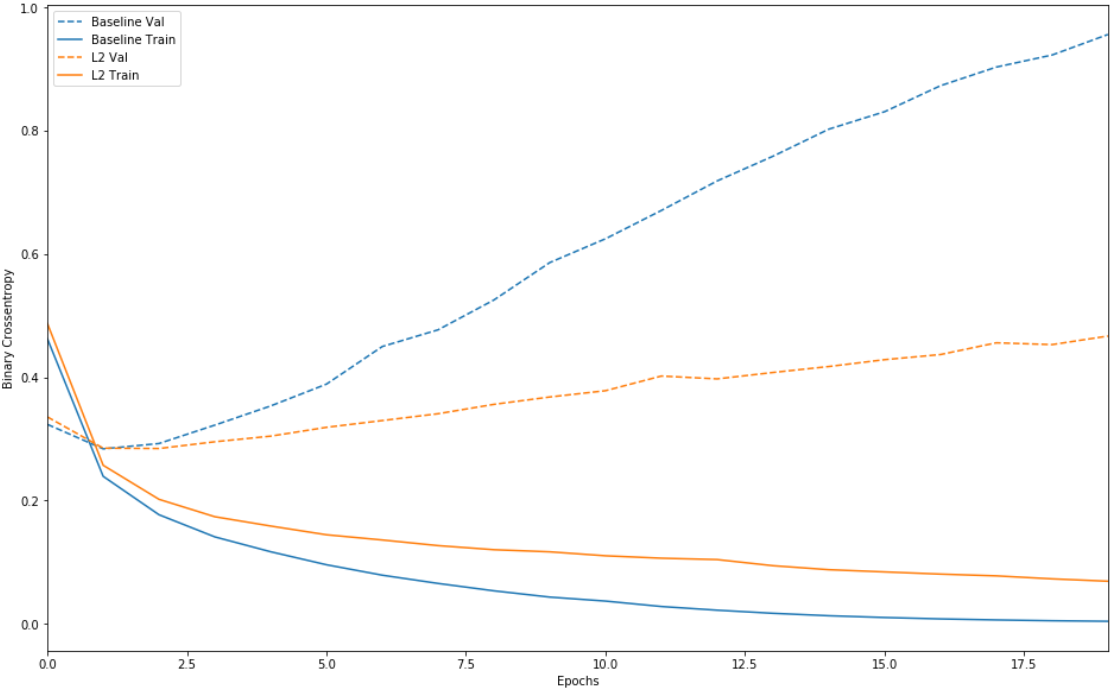
这样，正则项的确有效的降低了在测试集中的方差，没有产生严重的过拟合现象。

DropOut正则化

DropOut是随机丢弃的意思（应用于某个层），指在训练期间随机“丢弃”该层的多个输出特征。假设某个指定的层通常会在训练期间针对给定的输入样本返回一个向量 [0.2, 0.5, 0.3, 0.8, 0.7]；在应用丢弃后，取消低于某概率的神经元连接。

DropOut为何有效

在下一次的正向传播时，Dropout又开始运转，随机丢弃其他的层，所以每次传播时丢弃的节点是不一样的。假设某一神经元$x$接受的输入数为10，$x$就不会过分的依赖10个输入中的某一个，因为当过分依赖$y$时，$y$可能随机失活导致网络不够稳定，因此$x$对输入的权重依赖是均衡的。

在测试时，网络不会丢弃任何单元，而是将层的输出值按等同于丢弃率的比例进行缩减，以便平衡以下事实：测试时的活跃单元数大于训练时的活跃单元数。

简单的Tensorflow实现

在网络中添加两个丢弃层，看看它们在降低过拟合方面表现如何：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
dpt_model = keras.models.Sequential([
    keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
    keras.layers.Dropout(0.5),
    keras.layers.Dense(16, activation=tf.nn.relu),
    keras.layers.Dropout(0.5),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)
])

dpt_model.compile(optimizer='adam',
                  loss='binary_crossentropy',
                  metrics=['accuracy','binary_crossentropy'])

dpt_model_history = dpt_model.fit(train_data, train_labels,
                                  epochs=20,
                                  batch_size=512,
                                  validation_data=(test_data, test_labels),
                                  verbose=2)

plot_history([('baseline', baseline_history),
              ('dropout', dpt_model_history)])

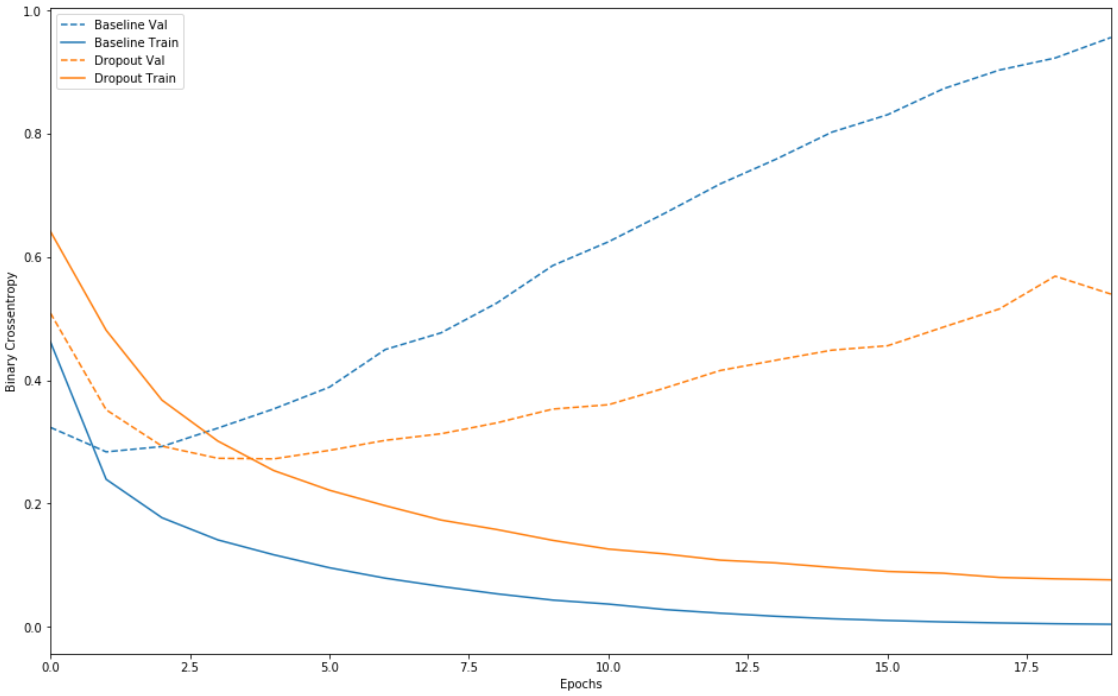
我们发现，效果还说的过去，在测试集中表现良好。

输入标准化

由于神经网络的层数很深，假设输入的是图像，那么传播到网络深层分布的变化会十分剧烈，模型的参数需要不断的剧烈变化去适应输入，还会造成梯度爆炸等现象。

正则化的输入与传播

其实对输入数据和网络中正向传播的数据进行标准化的处理，也能加快网络的学习速度。我们期望这个标准化可以去除特征之间的相关性；同时使得所有特征具有相同的均值和方差，做到独立同分布，并且希望这个操作可微分，且容易操作。先放上正则化的处理方式：

也就是每个特征减去自己的均值在除以自己的方差（测试是均值，方差保持一致），如果学过概率论的话，这样处理后的数据会服从均值为0，方差为1的正态分布，即$X\sim N(0,1)$，看下图：

优化意义

在机器学习中的一个重要假设independent and identically distributed (独立同分布，IID)，假设训练集与测试集是满足独立且相同分布，那通过训练集训练出的模型在测试集上能获得好的结果，也就是说模型具有泛化能力。但是若训练集与测试集的分布不一致，就叫做 Covariate Shift。Internal Covariate Shift 就是指神经网路内部各个层的数据分布不一致的问题。更详细的说明就是指神经网路的参数会随着每一层的训练更新，而每一次的参数更新都会使输入数据的分布产生变化，导致输出的分布改变，这个现象称为Internal Covariate Shift (ICS)。

因为每一层的参数都会受到前面所有层的参数影响，造成每层的数据分布不一致，导致神经网路要不断地学习新的分布，此外这些变化随着层数越深而越大，使得模型训练变得困难。过去为了解决这个问题只能设定较低的学习率(learning rate)，造成收敛速度过慢，而且因为每层的参数更新都会影响到后面层，因此每层更新的策略需要更谨慎。

当不对数据进行标准化时，比如特征$x_1$可能分布在$[1,1000]$，而特征$x_2$可能分布在$[0,1]$，这样的输入会使得成本函数分布在一个乱七八糟(左图)的空间内，可能会沿着最复杂的梯度进行下降，而对所有特征数据正则化到$[0,1]$区间内部时，此时数据之间对于结果的影响是相同的，能加快收敛。

使用Normalization 可以加速收敛，那在每层都使用Normalization，也就是指Batch Normalization 同样也可以加速收敛。另外，Batch Normalization 可以让每层的数据分布一致，让数值更稳定，因此可以使用较高的学习率优化，提高模型的学习速度。

此外，在网络的正向传播过程中，如果对网络的每一层的接受的输出(激活之前)也进行这样的处理，会激活到梯度变化最大的区域，减缓梯度消失。

传播过程对数据的标准化会使得参数$b$没有意义($x-\mu$)，所以也就取消了这个参数，而且还可以正则化为任意的均值和方差：

所以$\gamma$决定了方差，$\beta$决定了均值，也就是最终的数据分布是均值为 $\beta$，方差为 $\gamma^2$，保证模型的表达能力不因标准化而下降。这两个参数也是由网络学习而来(每层和每层不一样，测试时使用的$\mu,\sigma$为所有的batch的加权平均值)。

此外，当对数据进行正则化时，网络也能更加泛化。比如面临不同的输入：黑猫与白猫。网络在学习了认识黑猫后，可能还不认识白猫，因为两者的RGB数值差异很大。但是正则化会限制输入的均值与方差，保证了数据在$[-1,1]$范围内，也就是前层无论面临何种输入，对后层的权重影响都不会太大。通俗一些：由于Batch Normalization 是在每个 mini-batch 上做计算，而非在整个数据集上，可想而知每个mini-batch 的平均值与标准差有所不同，因此其平均值与标准差会有一些小噪音，也为神经网路训练的过程中添加了随机噪音。而这些轻微噪音与Dropout 所带来的噪音类似，因此Batch Normalization 也会有正则化的效果

不同类型的标准化

  • Batch Normalizatoin，对一个 batch 内的数据进行标准化，因此，BN 比较适用的场景是：每个 mini-batch 比较大，数据分布比较接近。在进行训练之前，要做好充分的 shuffle. 否则效果会差很多。但是对于目标检测、RNN 等领域不适用。
  • Layer Normalization，针对单个训练样本进行，取的是同一个样本的不同通道做归一化。不依赖于其他数据，因此可以避免 BN 中受 mini-batch 数据分布影响的问题。在 RNN 中的一个 batch 中，通常各个样本的长度都是不同的，当统计到比较靠后的位置时，这时只有一个样本还有数据，基于这个样本的统计信息不能反映全局分布，所以这时 BN 的效果并不好。
  • Group Normalization，分组标准化，组的数量可以设置为超参。在同一张图像上学习到的特征应该是具有相同的分布，那么，具有相同的特征可以被分到同一个 group 中，每一层有很多的卷积核，这些核学习到的特征并不完全是独立的，某些特征具有相同的分布，因此可以被 group 。

Python的简单实现

该层在每个batch上将前一层的激活值重新规范化，即使得其输出数据的均值接近0，其标准差接近1。

1
keras.layers.normalization.BatchNormalization(axis=-1)

利用numpy的广播机制快速对输入的数据标准化。

1
a = (a - np.mean(a, axis=0)) / (np.std(a, axis=0))

其他正则化方案

简单的介绍一种early_stop的方法，在测试误差达到最低点并开始上升的时刻终止训练，也就是在训练没有结束是提前结束训练过程。

Tensorflow的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class PrintDot(keras.callbacks.Callback):
    def on_epoch_end(self, epoch, logs):
        if epoch % 100 == 0: 
            print(epoch / 100)

EPOCHS = 500
# The patience parameter is the amount of epochs to check for improvement
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=200)
# Store training stats
history = model.fit(train_data, train_labels, epochs=EPOCHS,
                    validation_split=0.2, verbose=0,
                    callbacks=[early_stop, PrintDot()])

import matplotlib.pyplot as plt

def plot_history(history):
    plt.figure()
    plt.xlabel('Epoch')
    plt.ylabel('Mean Abs Error [1000$]')
    plt.plot(history.epoch, np.array(history.history['mean_absolute_error']),
           label='Train Loss')
    plt.plot(history.epoch, np.array(history.history['val_mean_absolute_error']),
           label = 'Val loss')
    plt.legend()
    plt.ylim([0, 5])
    plt.show()

plot_history(history)

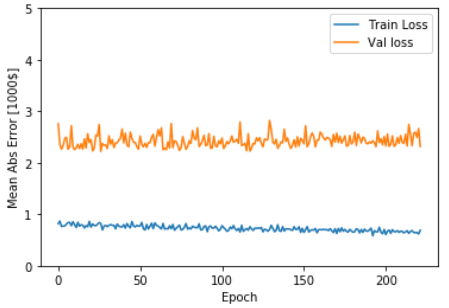
希望根据这些数据判断：对模型训练多长时间之后它会停止优化。此图显示，在大约200个周期之后，模型几乎不再出现任何改进。所以更新一下model.fit方法，以便在验证分数不再提高时自动停止训练。将使用一个回调来测试每个周期的训练状况。如果模型在一定数量的周期之后没有出现任何改进，则自动停止训练。

缺陷与不足

缺陷是什么呢？在之前的几种正则化方案中，降低成本函数$J(w,b)$和防止过拟合是两部分，但是early_stop中降低成本函数和防止过拟合成为了一部分，也就是为了防止过拟合，停止了训练，也停止了降低成本函数。这样得到的精确度不是最高的，但是训练速度可能比较快，在某些简单的场合也不是不能用。

本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章