2022 年 5 月 26 日回来复习。大概涵盖了这么多年写程序过程中遇到的梯度消失、梯度爆炸等基本情况，以及优化器的整理，后面会出一些为什么 train 到的神经网络准确率很低的文章。

有了梯度就要反向传播，而优化器对反向传播有着举足轻重的作用。这种东西之前很少接触，加上常年累月的直接调用，很多理论也忘记了。直到今天自己又去亲自探测了一番，恩，其实也不是不能接受。从统计学中的加权移动平均出发列举经受时间考验的优化器，和时间序列有异曲同工之妙，探求一下优化器的神奇之处。

梯度消失与爆炸

梯度消失相比梯度爆炸更为常见，梯度消失、梯度爆炸其根本原因在于反向传播训练法则，即在使用梯度下降法对误差进行反向传播时，由于求偏导累乘而出现趋于0（梯度消失）或者趋于无穷大（梯度爆炸）的问题。梯度消失和爆炸出现的原因经常是因为网络层次过深，以及激活函数选择不当，比如sigmoid函数

梯度消失：当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常；但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞；
梯度爆炸：当梯度爆炸发生时，初始的权值过大，靠近输入层的权值变化比靠近输出层的权值变化更快，就会引起梯度爆炸的问题；会导致模型不稳定，更新过程中的损失出现显著变化；

产生这些原因有很多：

网络初始化不好，relu 或者 sigmoid 激活后，位于梯度很小的区域，会出现梯度消失问题
损失函数选择不恰当，如 dice 损失，对于背景区域存在梯度为 0 的情况
网络层数很深，如果期间一直是 sigmoid 激活，梯度最大也就是 0.25，而多个 0.25 相乘，网络的浅层也会出现梯度消失。如果反向传播时，网络权重很大，累计乘法后就会出现梯度爆炸。

那么如何解决呢？

使用预训练模型，而后微调。如果不想使用预训练模型，就初始化模型参数
梯度正则化，限制梯度爆炸
relu 激活函数，解决了梯度消失、爆炸的问题，计算快，但负数部分恒为0，一些神经元无法激活。可以使用 leakrelu
使用 batch norm，激活后位于梯度不容易位于饱和区域
使用残差结构，解决梯度消失问题

优化器

加权移动平均
梯度消失与梯度爆炸
Adam，SGD，RMSprop，momentum，学习率衰减
简单的Tensorflow实现

这可能是我目前接触到的，变通和利用已有的知识进行问题转换较为成功的案例。对了，关于一些专业名词，比如eproch，batch，学习率等，可以来这里查阅：机器学习查阅手册

学习率衰减

普及一下随机梯度下降SGD就是，没使用一个样本就对网络权重更新一次，因为一个样本过于片面，所以导致成本函数在最小值附近徘徊但是很难收敛。

为什么难以收敛呢，这是学习率$\alpha$的原因，因为刚开始和最后结束$\alpha$是一直不变的，后期只要以$\alpha$学习了噪音数据，那么终究会导致函数值不够收敛，总是震荡。

所以，可以通过某种方式，规定在后期的$\alpha$会越来越小，也就是在后期能学习到的经验逐渐减少，强迫网络收敛。实现方式多种多样，举个栗子：

$\alpha=\frac{\alpha_0}{1+\mathrm{DecaryRate}\times \mathrm{eproch}}$

model.compile(optimizer=tf.train.MomentumOptimizer(
                            learning_rate=0.01,
                            decay=0.9
                            use_locking=False,
                            name='Momentum',
                            use_nesterov=False),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

实际上，在多位特征输入的情况下，很慢出现局部最优点的情况，出现局部最优就是函数为凸函数，而假设有100个特征(算比较少的了)，每个特征同时出现局部最优，此处出现局部最优解的概率为$2^{-100}$。

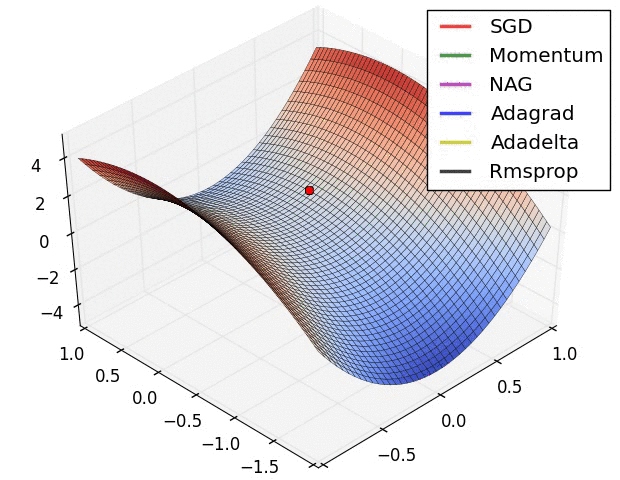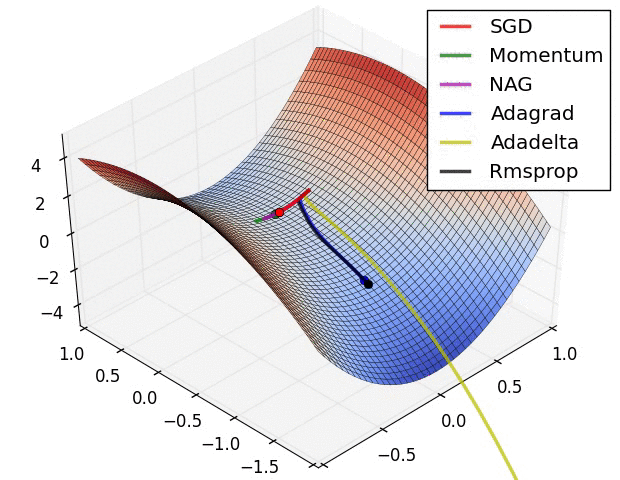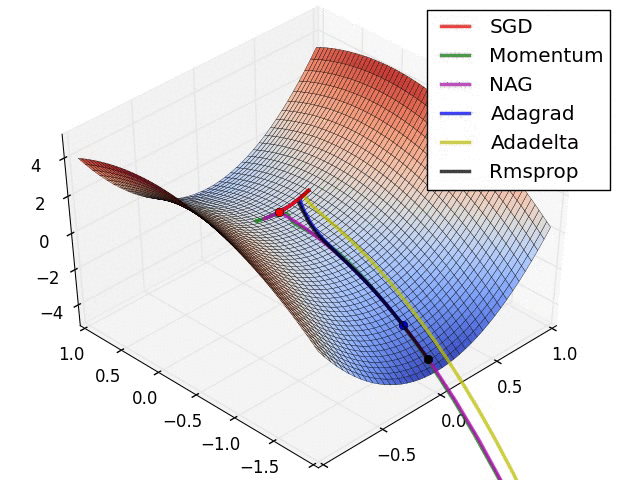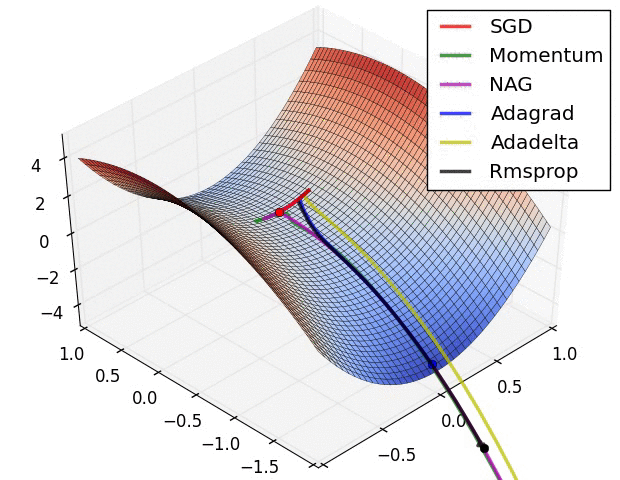
所以，更需要在意的是本文开头动画中马鞍面的处理。这个时候就需要一些强大的梯度函数来处理复杂情况了。

加权移动平均

给出加权移动平均的公式：

$v_n=\beta V_{n-1}+(1-\beta)x_n,v_0=0$

$x_n$是第$n$个数值，$v_n$是第$n$个的平均值，$\beta$是对前面数值的学习情况，因为设置初始值为0，前期的函数数值会偏低，不过这点误差可以接受。来看下图，首先产生一堆随机数，然后用不同的$\beta$去求随机数的平均值。

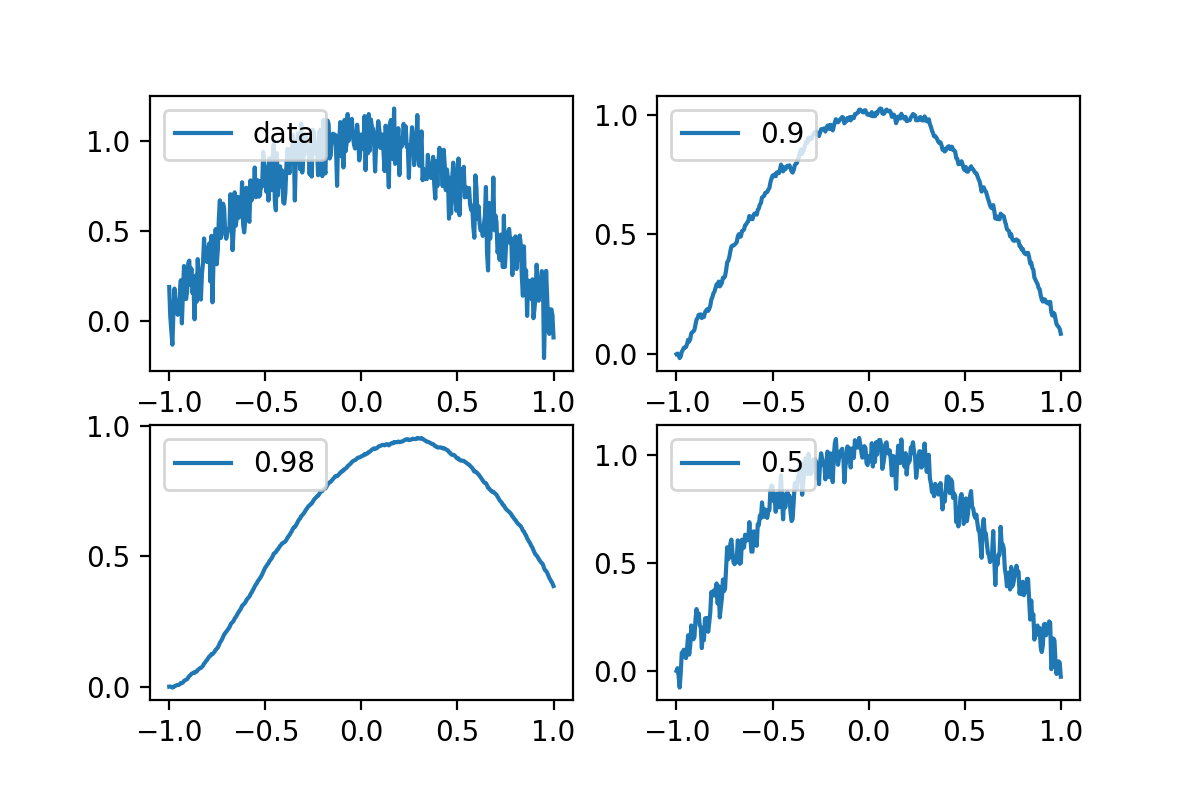
我们发现，当$\beta$过大的时候(0.98)，学习的趋势呈现出了随机性，而$\beta$太小时(0.5)，学习的趋势呈现出了滞后性，也就是对前面的信息学的慢，反应也慢。选择一个合适的$\beta$(0.9)，就能很好的描述出数据的平均走势。而接下来的优化器，也很大程度借鉴了这个观念。

python实现：

import numpy as np
import matplotlib.pyplot as plt

date = 365
x = np.linspace(-1, 1, date)
x = x.reshape(date, 1)
# 噪音数据
noise = 0.1 * np.random.randn(date)
noise = noise.reshape(date, 1)
# 产生随机函数
y = - x * x + noise + 1
# 加权移动平均函数
def weight__move_average(beta, date, y_value):

    v = [0] * date
    for i in range (1, date):
        v[i] = beta * v[i - 1] + (1 - beta) * y_value[i]

    return v

y_beta1 = weight__move_average(0.90, 365, y)
y_beta2 = weight__move_average(0.98, 365, y)
y_beta3 = weight__move_average(0.50, 365, y)

plt.subplot(2,2,1)
plt.plot(x, y, label='data')
plt.legend(loc='upper left')

plt.subplot(2,2,2)
plt.plot(x, y_beta1, label = '0.9')
plt.legend(loc='upper left')

plt.subplot(2,2,3)
plt.plot(x, y_beta2, label = '0.98')
plt.legend(loc='upper left')


plt.subplot(2,2,4)
plt.plot(x, y_beta3, label = '0.5')
plt.legend(loc='upper left')

plt.savefig('test.png', dpi = 200)

Momentum动量梯度下降

实际上，在使用batch输入时，因为存在噪音所以每时刻的梯度可能是一个乱七八糟的向量，就和上图的随机数一样。

但是更希望不学习乱七八糟的随机数，而是减少乱七八糟的震荡，描绘大体的趋势即可，这个时候，就可以借鉴上文的移动加权平均函数，对梯度也做这样的处理。

$V_w=\beta V_{w-1}+(1-\beta)w,V_0=0$ $w=w-\alpha V_w$

Tensorflow实现

实际上，tensorflow里面并没有上面的$1-\beta$这一项，tensorflow中的源码：

1 2	accumulation = momentum * accumulation + gradient variable -= learning_rate * accumulation

创建动量梯度下降优化器：

from tensorflow import keras
import tensorflow as tf

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation=tf.nn.relu),
    keras.layers.Dense(10, activation=tf.nn.softmax)
])

beta = 0.9

model.compile(optimizer=tf.train.MomentumOptimizer(
                            learning_rate=0.01,
                            momentum=beta,
                            use_locking=False,
                            name='Momentum',
                            use_nesterov=False),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

RMSprop

为了下文的简便，这里先将上面的$v_w$暂时更换为$s_w$。同上，RMSprop只是在momentum的基础上改进了一点点：

$s_w=\beta_2S_{w-1}+(1-\beta_2)w^2$ $w=w-\alpha\frac{w}{\sqrt{s_w}}$

在上面的两个式子中，我们发现当$w$很大时，$s_w$也会很大，当$w$很小时，$s_w$也会很小，这就保持了在$w$更新时较为平稳，减缓不恰当的摆动。

Tensorflow简单实现

beta2 = 0.9

model.compile(optimizer=tf.train.RMSPropOptimizer(
                            learning_rate=0.1,
                            momentum=beta2,
                            epsilon=1e-10,),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

Adam优化器

其实，把momentum和RMSprop整合一下爱，就得到了Adam优化器：

首先初始化：

$v_w=0,s_w=0,v_b=0,s_b=0$

然后加权移动平均：

$v_w=\beta_1v_{dw-1}+(1-\beta_1)w \qquad v_b=\beta_1v_{b-1}+(1-\beta_1)b$ $s_w=\beta_2s_{dw-1}+(1-\beta_2)w^2 \qquad s_b=\beta_2s_{b-1}+(1-\beta_2)b^2$

根据学习率对参数进行刷新：

$w=w-\alpha \frac{v_w}{\sqrt{s_w}} \qquad b=b-\alpha \frac{v_b}{\sqrt{s_b}}$

简单的Tensorflow实现

1
2
3

model.compile(optimizer=tf.train.AdamOptimizer(),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

结语

通过这几天的整理，生动形象的诠释了什么叫先看懂数学原理再来抄代码，不然代码的参数，含义都看不懂，Ctrl c和Ctrl v来的代码没有灵魂，无非是某些培训机构让你快速入门的盈利工具。

实在是不能再折腾这些乱七八糟的了，得赶紧看高数了，不然考不上研究生了刺激。

其实还有某些网络的调控方案，梯度消失梯度爆炸的问题，简单描述一下吧。

在调教网络的时候最好不要先调一些玄学的参数，而是先看看训练误差，测试误差是否达标，训练误差高就换网络提强特，测试误差高就对网络正则化。如果训练集和测试集来源不同，最好还是取测试集一部分并入训练集，毕竟是在训练集上训练网络的。而且还有观察判别错误的数据，分析原因。至少要知道哪里出问题了，然后对症下药。

梯度消失和梯度爆炸，就是在网络长时间的传播过程中出现的参数巨大或参数无限接近于零的情况，这个时候参数会出现巨大的变动或者几乎不变的情况。如何避免呢？一个是有效的初始权重，使得权重在1附近，毕竟$1\times 1=1$，或者，对权重的正则化，对权重的剪枝将梯度值限制在某范围内，使用relu激活函数，毕竟这个函数的激活范围导数恒等于1。

Just for Life.

神经网络中的梯度