内容简介:在阅读了数据结构的一本教材《大话数据结构》后,学到了新的姿势:用于搜索引擎的数据结构——倒排索引,又想起了曾经在《数学之美》上阅读过的如何在搜索引擎中取得高质量的网页和最相关的内容。涉及到了简单的分词、矩阵相乘、信息熵的简单应用,特来整理,即使我做不出一个搜索引擎。但是在现实世界中的应用多种多样,背后的数学思维却是可以借鉴的。(注明:本文只是将两书的内容融会贯通并整理。如有遗漏使得内容看起来不连贯,可以阅读原书,计算机专业推荐这两本书都读,非计算机专业只推荐阅读《数学之美》)
倒排索引
引言
以下内容只是简单的举例,先来看两个简单的句子:
- Iron Man is a 2008 American superhero film based on the Marvel Comics character of the same name.
- Captain America is a fictional superhero appearing in American comic books published by Marvel Comics.
假设上面两个句子是两个网页里面的内容吧。当创建新的网页部署到因特网上的时候,形如谷歌、必应等引擎会第一时间派遣爬虫机器人来获取你网页上的内容,比如各种单词的数量,单词内容等。将获取到的信息添加到谷歌内部的数据库里面。当某一用户使用谷歌搜索时,谷歌根据自己内部数据库的东西,进行各种算法,给出你想要的结果。
形如各种常用的搜索引擎,即使待推荐的网页里面有一万个单词,但是搜索的时间都不会很长。显然并没有去遍历每个网页来确定是否推荐,而是设立了一种合理的数据结构来加快搜索进程。这个数据结构就是倒排索引。
实例
对于上面两个句子,一共有二三十个单词。假设有33个单词吧,我懒得数了,那么我们就建立一个33长度的表。那么 Iron Man 是 1 中特有的单词,fictional 是 2 中特有的单词,superhero是 1 和 2 供有的单词,那么得到下面的表。
| 单词 | 索引 |
|---|---|
| Iron Man | 1 |
| fictional | 2 |
| superhero | 1, 2 |
当有新的网页时就增加第三个网页,记为 3 。当然在后期处理的时候,单词的过去式、正在进行时、被动词等可以视为一个单词。当用户在引擎中输入搜索的内容时,比如superhero,那么就会搜索superhero在哪里出现。superhero在1, 2 中出现,那么就把1, 2 推荐出去。由此可见,这个方式根据内容确立索引顺序,而别的排序方式(脑补斗地主整理牌是有顺序的)是根据索引顺序确定牌的位置。和别的排序方案的逻辑相反,因此称为倒排索引。
优化
- 这个词表可以使用基数排序增加查询速度(基数排序就脑补新华字典的按拼音排序,一个道理)。
- 词表不仅仅存储单词在哪里出现,还可以包括单词在该网页中出现的频率等等。
- 这个表的后期维护也需要很大的努力,起码得精通数据结构中的查询、插入等操作吧。
筛选最相关
思考
其实还有问题,比如搜索的问题是:application of time crystal 。相对而言,形如 of , a, an, the 等介词出现频率虽然很高但是并无卵用。application 和 time 是常用词,也是很多背景下的应用词。crystal 虽然是不常用词汇,出现频率也很低,但是却能体现查询的核心含义。如果关于crystal 的链接很少,pagerank出来的结果都是关于application of time的,那么这个查询岂不是要凉?接下来接着填坑,这个坑填完后一个简朴的搜索引擎就完成了,但是实际中的搜索引擎还需要很多细节的技术需要完善,比如是不是要考虑点击量。
假设查询application of time crystal, 有三个网页是关于时间晶体的,有100个网页是关于时间应用的。这103个网页都是高质量网页,但只有3个网页才是真正想要的网页。既然确定了目标,就想办法整俩公式把问题解决掉。然后传说中的TF-IDF算法诞生了。
- 一个词预测主题的能力越强,它的权重就应该越大,反之权重越小。在网页中的“时间晶体”这个词,或多或少可以推测出查询内容。但是看到“应用”一词,还是不知道想要查询什么。
- 形如 “的” “啊” “和” 等停用词权重为零,日常修饰语在查询的时候没有用的。
推导
一个查询中的每一个关键词应该反应出:这个词对查询提供了多少信息。如果一个查询包括$N$个关键词,他们在一个网页中的出现频率是:$TF_1,…,TF_n$,$N$是语料库的大小。以每个词的信息熵作为它的权重。
之后,如果两个词的频率相差无几,一个词(时间晶体)是某篇文章的常用词,另一个词(应用)分散在多篇文章中,显然前者的权重应该更大,提供更好的分辨率。那么开始下面的表演:
假设每篇文章的单词数是$M$,$D$是pagerank后的全部网页数量。则$M \cdot D = N$。
一个关键词在一个文献中出现的次数为:$c(w)=\frac{Avg(TF(w))}{D(w)}$。推导出:
继续,一个词的$I(w)$越大,相似性越大,一个词的平均出现次数越多,相似性越小。两者做个减法在做进一步处理,得到TFIDF的公式
看两个等号之间的式子,第一项越大越好,第二项越小越好,推导出了新的式子。
而新的式子$\mathrm{TFIDF}=TF(w)\log \frac{D}{D(w)}$也是现在最常用的方案。$TF(w)$是词频率,含义为某个词在文章中的次数除以文章总词数,而IDF的英文是inverse document frequency,逆文本频率指数,公式是$\log \frac{D}{D(w)}$,含义是语料库的文档总数除以含有该词汇的文档数后取对数。
其实是先给出的TF-IDF公式,多年后信息论发展起来才用信息熵证明了IDF公式为什么这么写,是用$\log$ 而为什么不是根号。本文是直接从证明开始,引出的IDF公式。没想到数学还能严谨到如此境界,我还是好好用数学吧,我这脑子研究不了数学。
最终,计算一篇文章每个词汇的$\mathrm{TFIDF}$并排序,取其中$\mathrm{TFIDF}$值最大的词汇,作为文章的关键词,即提取出一篇文章的几个关键词。
计算相似性
既然求出了每篇文章的代表词汇或称为关键词,仅仅需要计算查询的词汇和每篇文章关键词的相似度即可。这里使用余弦定理进行计算,当然也可以使用自然语言处理。
众所周知余弦定理可以计算两个向量的相近程度,两向量重合,则相似度为1,两向量垂直,则认为没有相似性。利用这个原理,很可以推导出如何将句子映射为向量:
- 句子A:我喜欢看电视,不喜欢看电影。
- 句子B:我不喜欢看电视,也不喜欢看电影。
而后将两个句子合在一起进行分词:我,喜欢,看,电视,电影,不,也。
计算词频:
- 句子A:我 1,喜欢 2,看 2,电视 1,电影 1,不 1,也 0。
- 句子B:我 1,喜欢 2,看 2,电视 1,电影 1,不 2,也 1。
写出词向量:
- 句子A:[1, 2, 2, 1, 1, 1, 0]
- 句子B:[1, 2, 2, 1, 1, 2, 1]
而后就可以计算两个句子的相近程度了。如果你还不能理解,我在举个极端的例子。
- 句子A:是。
- 句子B:否。
很容易得到句子A的词向量是[1, 0],而句子B的词向量是[0, 1],这两个向量垂直,相似度为0。
代码
没有找到合适的数据,就自己创造的没有link的数据,所以本次代码因缺数据而没有加入pagerank算法的代码。
倒排数据结构展示:
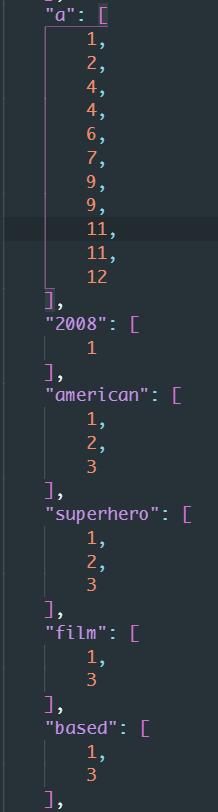
查询结果输出展示,对输入的内容进行查询。
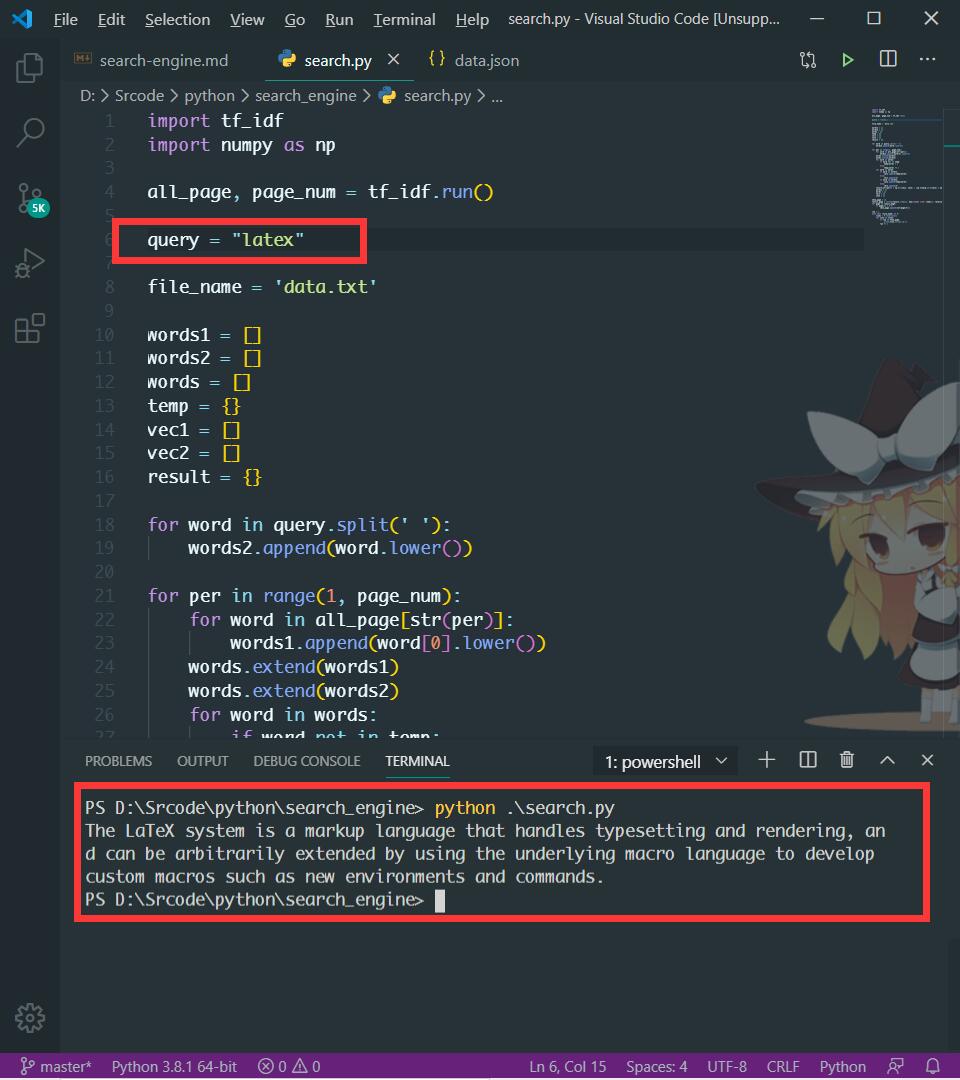
结语
至此,从开始的倒排索引寻找出所有满足需求的网页,再用pagerank从满足需求的网页中求出高质量网页,在用TF-IDF算法在高质量网页中求出和查询最相关的网页。一步步完善,将自然语言以恰当的方式转为数字进行处理。当然还需要更详细的处理步骤,比如网页的反作弊技术,比如点击量,如何屏蔽相似性很高的广告等等。
计算机和数学的应用层出不穷,即使也存在过时的技术,比如pagerank已经被谷歌淘汰,但背后的数学思维值得我们借鉴。比如2019年的美国大学生数学建模竞赛的C题,如何确定毒品的传播源头,不就是pagerank可以应用的场景吗。
其实还有坑的,比如使用中文查询:“什么是汇编语言的中断”,那么新的问题又来了。英文单词之间有分割,自动提取关键词。中文的是句子呀,怎么让计算机认识句子并从里面抠出关键词呢?下次再写吧,这就涉及到了一些中文的自然语言处理的知识了。

