假期实在无聊,开始整理过去的文件,发现了自己原来是数学建模起家的。长话短说,翻阅了在过去时间里自己做过的模拟题,所有的模型是自己设计的,代码也是自己写的。而倾注了自己心血的东西,难免会有些有意思的地方。比如:
- 数据缺失,如何去除,如何补充,哪些去除,哪些补充,都是有学问的;
- 另外就是今天的主角,元胞自动机——万物皆可模拟。
另一方面是,当初在学习元胞自动机这个模型时,网上的资料是在少之又少,且内容凌乱的不堪入目,我猜作者也不知道他在写啥,自己也走了很多弯路。遂决定,以实战的背景,演示元胞自动机的工作原理和使用方法。而在看本文之前,你只需要知道元胞自动机里面有很多格子,格子间通过某种规则相互影响即可。

引言
模拟题是2015年的MCM的A题,决定用元胞自动机去模拟埃博拉病毒的传播。但我不会把论文的全部内容放上来,只写关键的文字,什么参考文献,数据网址就不放了。且时过境迁,本文使用的数据为过去式,和今天对不上则选择性忽略。
The world medical association has announced that their new medication could stop Ebola and cure patients whose disease is not advanced. Build a realistic, sensible, and useful model that considers not only the spread of the disease, the quantity of the medicine needed, possible feasible delivery systems (sending the medicine to where it is needed), (geographical) locations of delivery, speed of manufacturing of the vaccine or drug, but also any other critical factors your team considers necessary as part of the model to optimize the eradication of Ebola, or at least its current strain. In addition to your modeling approach for the contest, prepare a 1-2 page non-technical letter for the world medical association to use in their announcement.
代码的原作者和链接:https://zeroto521.github.io/2018/09/23/MVC.html
符号说明
- $v_{psd}$:病毒传播速度。在正式确定埃博拉病毒导致疾病后,截止于2014年12月31日,每天感染病毒的人数。
- $\eta_1$:埃博拉病毒的感染率,即与携带埃博拉病毒的宿主接触后被感染的几率。
- $\eta_2$:埃博拉病毒的死亡率,即感染埃博拉病毒后的死亡几率。
- $N$:三个国家总人数。1181万。
- $N_1$:三个国家的感染人数
- $N_2$:三个国家的死亡人数
模型假设
- 假设我们运输药物的路径可以视为直线。
- 假设在治疗疫情期间,运输药物的车辆、直升机等可自由穿越国界。
- 疫情传播并不会因国家不同而传播方式不同,因此假设三个国家的死亡率、感染率相同。
- 后期分配药物建立运输系统时,考虑到疫情的严重性,及生命的重要性,我们会将三个国家视为一个地区。
- 假设三个国家的所有机场、港口均能使用,且在疫情期间内能够支持药物的运营。
- 在根除西非区域的埃博拉病毒时,假设病毒患者在家中、医院或隔离区,视为静止点。规定医疗人员前往静止点进行救治,而不是感染患者来急救站点进行救治,防止因感染人员流动而导致病毒扩散带来的不良后果。
前期工作
元胞自动机
后文的元胞自动机均简称为CA。
CA(Cellular automaton)具有模拟复杂系统演化过程的能力,以网格代表不同的状态,通过定义相关的规则来模拟真实世界的发生情况,不用考虑复杂的计算公式,只需通过网格之间的规则来模拟真实情况因而在社会学、物理学、化学领域都有广泛的应用。
SIR状态
在最简单的情况下,按照区间可以将人群分成两个健康状态:易感染病原体(通常用$S$表示); 感染的病原体(用符号$I$表示);免疫体状态(用符号$R$表示)。因此,我们基于元胞自动机设立演化规则,呈现病人的SIR状态,模拟埃博拉病毒的传播。
埃博拉病毒
考虑到不同地区的卫生条件、对疫情不同的控制方式,因此难以给出明显的函数关系式来描述所有情况下人口密度与疾病传播的内在联系。
埃博拉病毒能够通过各种渠道进行传播,通常潜伏期为5-10天,并且有极高的致死率。埃博拉病毒爆发于塞拉利昂国家东部与几内亚和利比里亚同时接壤的区域。病毒首先从人口密度大的爆发起点城区区域感染,然后向外扩散。距离爆发区域近的人口密度小的森林区域感染程度处于中等水平,而距离爆发区域近的人口密度大的城区区域感染程度处于较高水平。总体来看病毒感染水平随着距离爆发起点区域的距离越远感染程度越低,森林区域的病毒感染水平要比附近的城区区域低。
建立模型
以SIR状态为CA模拟病毒传播时元胞状态的表现形式。在埃博拉病毒初期传播过程中,因没有完全有效的抵制病毒传播的有效疫苗和药物,因此不考虑完全免疫个体,但存在临时免疫的个体,即在康复后仍然具有被感染的概率。由此,结合传统的SIR“易染-感染-移除”(Susceptible-Infected-Removed)模型,建立符合实际情况的“易染-感染-死亡-暂时免疫”(Susceptible-Infected-Dead-Temporarily immunized)模型,进而模拟埃博拉病毒传播的实际情况。即网络节点被假设成以下的四种状态:
- 易感状态$S$,不会传染其他人,但是有几率被感染;
- 感染状态$I$,已经患病且具有传染性
- 死亡状态$D$,因感染疾病而死亡,且死亡后若尸体处置不恰当,仍然能够传播病毒
- 暂时免疫状态$T$,因采取及时隔离、药物治疗等措施,病人暂时康复,但是没有长期的抵抗力。
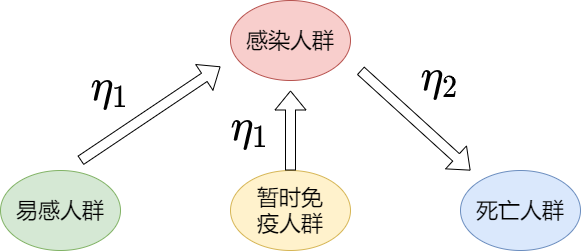
定义CA规则
定义CA格子表达含义
因埃博拉病毒的传播过程中,每一个国家均存在感染病毒的几率与感染病毒后的死亡几率,不会受到地理空间分布的影响,用CA表示国家的空间分布没有实际意义,因此不考虑用元胞空间表示实际地理空间。
在前期工作中,我们了解到在一个区域内,会因人口密度、人口数量不同,而导致感染水平不同。即在人口密度大的城市,感染水平会高于人口密度低的城市,人口密度在很大程度中影响疾病传播率。因此元胞自动机模拟埃博拉传染过程中,设定CA的每一个方格代表人口密度,并且每个方格所代表的人口密度相同。并根据三个国家的人口数量比例划分元胞空间,划分域如下。
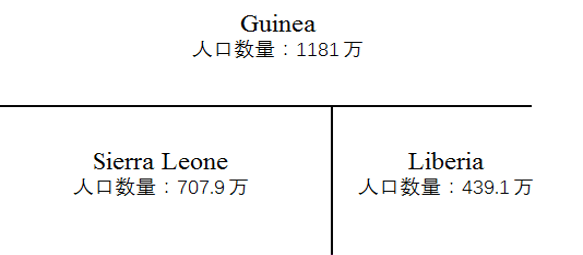
定义CA颜色含义
- 缺少计算服务器,因此元胞数量设置为$20\times 20$,用于表示并模拟区域内疾病的传播,进而得到患病者死亡率、感染率的分布规律。并且定义灰色表示死亡状态;红色表示已经被感染状态,且颜色越深代表被感染时间越长;白色表示易染状态和暂时免疫状态。
定义CA迭代含义
- 假设 CA 的迭代次数$i$时,每一次迭代可视为模拟的埃博拉病毒传播$\lambda$天的传染效果,其中$\lambda$为迭代一次代表的时间长度,则$\lambda=365/i$。
定义CA中人口流动的频率与范围
- 在埃博拉病毒的爆发之际,病毒主要的传染方式为人口的流动导致病毒的扩散,进而导致各地区开始出现疫情,最终导致疫情恶化而难以控制。因此,我们需要考虑人口流动现象对疫情的影响。在疫情初期,人口流动的频率$F$与范围$R$会高于疫情严重时期人口流动的频率与范围。流动半径$R$在CA中的表达形式为:格子的数量。流动频率$F$在CA中的表达形式为:在时间长度为100天的期限内,发生人口流动现象的天数。因随着时间的增加,疫情逐渐严重,人口流动频率会逐渐降低,符合指数分布的特征,设符号$t$表示疫情爆发时间,则流动频率的表达式为$F(t)=\frac{1}{\theta}e^{-t/\theta}$,$\theta$为参数。
数学表达CA所需的参数
理论死亡率
埃博拉病毒传染具有潜伏期,潜伏期的时间通常为为5-10天,过了潜伏期之后便会死亡,因此感染时间越长,死亡率越高。当被感染埃博拉病毒的人足够多时,可认为潜伏期$\phi(t)$服从正态分布$N(\mu, \sigma^2)$,$\mu=7.5, \sigma^2=1$为假定参数。以易染状态的元胞$i$举例,若在第一次迭代后被感染变为状态$I$;第二次迭代以$\Phi(5+\lambda)$的概率变为死亡状态( 为迭代一次所代表的时间长度);第三次迭代以$\Phi(5+3\lambda)$的概率变为死亡状态,以此类推第j次迭代后以$\Phi(5+(j-1)\lambda)$的概率变为死亡状态。

理论治愈率
实际情况中,国家政府会对埃博拉病毒采取一定的抵抗措施,因此定义治愈率函数$f_1(t)$,治愈率包含自身对埃博拉的抵抗力,以及国家对疫情的控制情况,如隔离、医疗救助、及时医治等措施能够减缓疫情的蔓延率与死亡率。
因自身免疫力与国家对疫情控制度共同影响了死亡率,而在前期调查中得知三个国家的死亡率并不相同,三个国家死亡率分布:利比里亚死亡率$\eta’=42.7\%$,几内亚死亡率$\eta’’=63.1\%$,塞拉利昂死亡率$\eta’’’=29.2\%$。
当元胞$i$变为感染状态$I$时,随着时间增加,治愈系数会逐渐减弱。假设这种减弱的关系服从指数分布,则治愈函数$f_1(t)$的表达式为$f_1(t)=\frac{1}{\theta_1}e^{-t/\theta_1}$。而实际中三个国家的治愈系数并不相同,为反应出三个国家治愈率的不同之处,用三个国家的死亡率进一步表示治愈率,得到如下的关系式:
理论死亡率与康复率分布图如下:
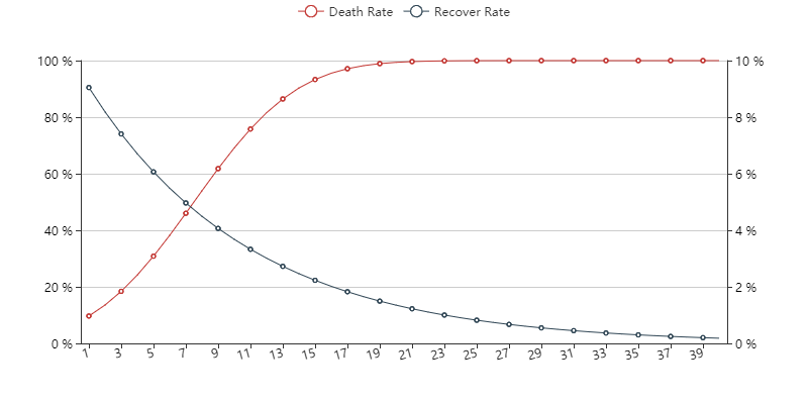
计算真实死亡率与真实治愈率
计算真实死亡率与康复率:目前只提出了理论死亡率与理论治愈率的计算方法,因假设死亡率随时间增加符合正态分布,因此死亡率会逐渐增加,并十分接近100%,因此提出的理论情况并非真实情况下的死亡率与康复率。在实际情况中,当死亡率很高时,仍会有个体康复;在个体康复率很高时,仍会有个体死亡;为表示这一关系,采用下列方程式计算真实情况下的康复率与死亡率:
| 分类 | 真实治愈率$O_1$ | 继续被感染率 | 真实死亡率$\eta_3$ |
|---|---|---|---|
| $f_1(t)>\Phi$ | $\frac{1}{t}e^{f_1(t)-\Phi}\sqrt{f_1(t)-\Phi}$ | $1-O_1-\eta_3$ | $\frac{t}{t+\epsilon}e^{\Phi-f_1(t)}\sqrt{f_1(t)-\Phi}$ |
| $f_1(t)<\Phi$ | $\frac{1}{t}e^{f_1(t)-\Phi}\sqrt{\Phi-f_1(t)}$ | $1-O_1-\eta_3$ | $\frac{t}{t+\epsilon}e^{\Phi-f_1(t)}\sqrt{\Phi-f_1(t)}$ |
$\frac{1}{t}$和$\frac{t}{t+\epsilon}$为时间修正公式:$\frac{1}{t}$是减函数,随时间增加而减小,用于修正康复率,则康复率随感染时间增加而减小;$\frac{t}{t+\epsilon}$是增函数,随时间增加而增加,用于修正死亡率,则死亡率随感染时间增加而增加,更具真实性。
$e^{f_1(t)-\Phi}$为概率修正公式:在理论治愈率$f_1(t)$大于理论死亡率$\Phi$时,有一定几率死亡,也有一定几率康复;当$\Phi$大于$f_1(t)$时,仍有一定几率被治愈;但$f_1(t)+\Phi$可能高于100%,且死亡率与康复率之间存在着继续感染的几率。因此,需要将理论死亡率$\Phi$、治愈率$f_1(t)$进行变换为$e^{f_1(t)-\Phi}$,得到更接近实际的死亡率与治愈率,并求解继续感染的几率。
借鉴模拟退火算法的思想,在解空间内以一定的几率发生跳变,即某种事件发生的概率较低时,仍能有一定几率发生。因而,在$\Phi$大于$f_1(t)$时,康复的概率修正为$e^{f_1(t)-\Phi}$,当$\Phi$小于$f_1(t)$时,死亡的概率修正为$e^{\Phi-f_1(t)}$。
$\sqrt{f_1(t)-\Phi}$为误差修正公式:当$f_1(t)<\Phi$且$f_1(t)$接近于$\Phi$时,存在
的现象,得到了当死亡率接近康复率时,康复率接近于1的错误结论。为避免这种现象的发生,增加修正项$\sqrt{\Phi-f_1(t)}$,当$f_1(t)\rightarrow\Phi^{-}$时,$e^{\Phi-f_1(t)}\sqrt{\Phi-f_1(t)}$趋于稳定(不是高数题,没那么无限趋近于0),因此避免治愈率接近于死亡率时概率计算错误现象。
开始CA模拟
当元胞$i$为状态$S$时,若它的邻居中存在感染者(即有状态$I$的邻居),则在下个时间步里,元胞$i$的状态以概率$\eta_1$变为被感染状态$I$。
对尸体处置不当,导致尸体仍然能继续传播埃博拉病毒的情况,因此假设死亡元胞$i$会以概率$\eta_2$感染其他元胞。
当元胞$i$为状态$I$时,元胞$i$会以概率$\eta_3$由感染状态变为死亡状态。
当元胞$i$为状态$I$时,元胞$i$会以概率$O_1$由感染状态变为暂时免疫状态$T$。
同时暂时免疫状态会以概率$\eta_1$再次变为被感染状态$I$;
结果分析
采用定义的CA规则,对2014年内埃博拉爆发情况进行模拟,当CA迭代完成后,得到如下的结果,其中灰色代表死亡状态,白色代表易染状态,红色代表被感染状态,颜色越深表示被感染程度越高。

如图所示,每一个方格代表感染人口,埃博拉病毒迅速传染至每个区域,区域内人口开始出现感染埃博拉病毒以及死亡的现象,并且在国家政策干预和患者自身免疫力的抵抗下,在感染区域内仍有康复个体。
我们计算元胞自动机模拟结果中几内亚感染数(GI)与几内亚死亡数(GD)比例,塞拉利昂感染数(SI)与塞拉利昂死亡数(SD)比例,利比里亚感染数(LI)与利比里亚死亡数(LD),总感染案例(TI)与总体死亡数(TD),(格子数乘以对应人口密度)。并与原始数据对比,得到的对比情况如下图。
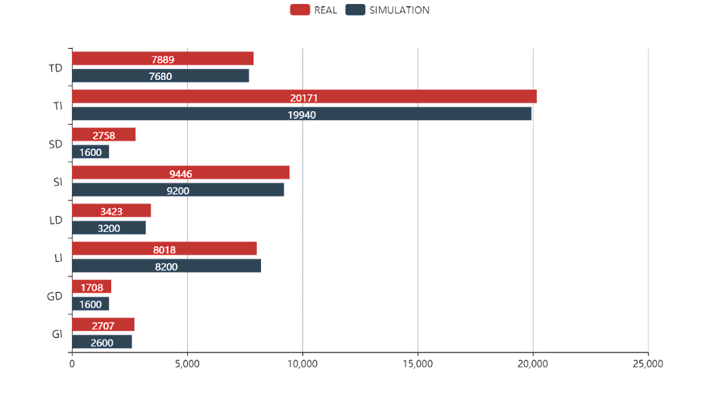
与实际情况对比之下,发现我们建立模型的模拟的效果较好,与实际结果极为接近,并且证实了之前假设的合理性。并根据实际数据调节模型中的参数,最终调整参数的结果为:传染率:$\eta_1=0.8$ ,死亡传染率:$\eta_2=0.15$,时间修正函数:$\epsilon=10$,迭代步长:$\lambda=1$,游走频率指数分布中$\theta=5$,游走半径$R=2$,治愈率指数分布$f_1(t)$中,$\theta_1=10$,理论死亡率的正态分布$\phi(t)$中:$N=7.5, \sigma^2=5$。
开始治疗
假设采用空运的形式将疫苗从制药工厂送往区域E内的所有机场。针对疫情最为严重的三个国家,在Google Map中我们查询到疫情覆盖范围内最远距离为1135公里左右,假设以直升机或卡车的方式进行运输,则在一天内足够将药物送到我们设立的急救站点处,因此不再考虑运输药物时间对疫情的影响。
创立良好的医助条件:①当地政府需要指挥相关人员配合医生,及时对染病患者进行隔离,建立隔离区或在医院对患者进行隔离,防止疾病传播疫情难以控制;②在对患者进行救治时,将救治好的患者及时脱离隔离区,避免二次感染;③对因感染疾病而死的患者尸体,及时进行有效的火化处理,防止尸体传播病毒。
治疗模型建立
假设此时已经开始建立良好的医疗条件,如:隔离、焚烧尸体等。
改进感染率
在实际情况中,当周围被感染埃博拉病毒的人数较少时,若及时对染病人群就进行隔离,则病毒对易感染人群的感染率较低;若一个区域内疫情严重爆发,染病人群远远高于易染人群,则病毒对易染人群的传染率会相对较高。为在CA中描述这种关系,建立以下数学模型。
在最初的CA中感染率为固定参数,病毒仍以固定的感染率在元胞之间进行传播。在状态为$S$(易染)的元胞附近,没有充分考虑状态为$I$(感染)的元胞数量对传染率的影响,即$S$状态元胞附近被感染的元胞数量较多时,传染率会有所改变而并非常数。
因此,假设元胞$i$处于$S$(易染)状态,在近邻8个元胞方格中有$\Psi(0\leq\Psi\leq 8)$个元胞处于$S$(感染)状态,有$\xi(0\leq\xi\leq 8)$个元胞处于死亡状态,但因及时有效对尸体进行火化处理,死亡状态不会在传染病毒,因此$\eta_2=0$。则元胞$i$以$P$的概率被感染,其中$P=\frac{1}{8}(1+k)(\eta_1\Psi)$,$k$为参数。
增加药物治疗效果
随着感染时间的延长,病情逐渐恶化,药物的有效率逐渐降低。若患者第一天被感染病毒,设药物的有效率为$\beta_0$,患者处于潜伏期最后一天时药物有效率为$\beta_n$,则$\beta_n > \beta_0$。假设药物的有效率与时间变化仍服从指数分布,则有效率随感染期限的变化函数为$f_2(t)=\frac{1}{\theta_2}e^{-t/\theta_2}$,$\theta_2$为参数,$t$为感染时间。
在最初CA模拟疾病爆发时,疫情的蔓延和死亡受到治愈率的影响,而在对患者使用药物后的治愈率同样会提高。药物的治疗率为$f_2(t)$,初始治愈率为$f_1(t)$,但对于病人而言,最终的药物治疗效果并非简单叠加:$f_1(t)+f_2(t)$,因为这会导致康复率大于1,出现完全治愈的现象,不符合实际情况。因此假设药物治疗效果与国家监管对治疗患者的成功率存在交互影响作用,此交互影响作用表达式为$(1-\alpha)(f_1(t)+f_2(t))$,$\alpha$为交互因子,因此,得到使用药物后的治愈率:$f_3(t)=(1-\alpha)(f_1(t)+f_2(t))$。
模拟结果
根据模拟2014年埃博拉爆发得到的不同区域内元胞的感染状态与死亡状态,并以此为基础,加入药物治疗因素影响,在感染与死亡基础之上进一步模拟药物治疗效果,随迭代时间增加,感染率逐渐降低,被感染的患者也被医治好,得到如下的药物的治疗效果。
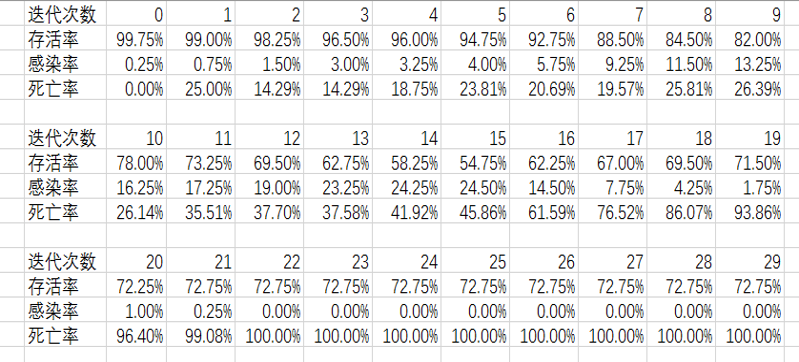
感染率由最初的24%逐渐降到0%。
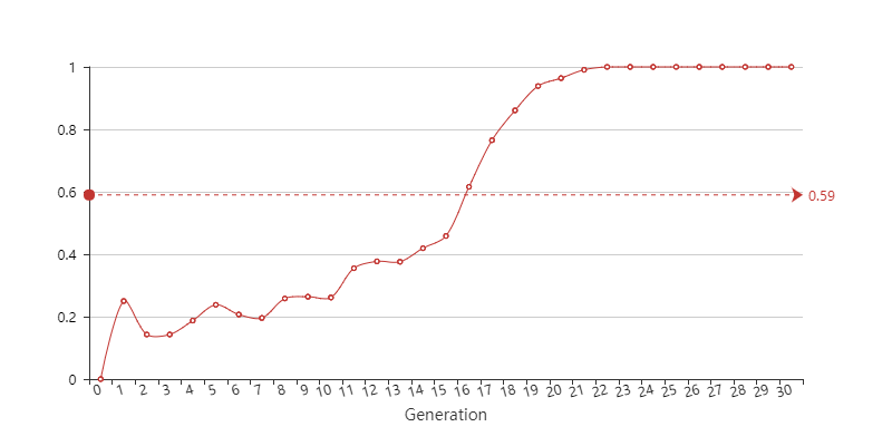
在CA迭代15次时,模拟的是2014年内埃博拉爆发时死亡情况与感染情况,感染率达到高峰;在迭代15次之后,加入药物治疗因素影响,模拟加入药物对埃博拉疫情的根除效果,感染率逐步降低。感染率示意图如下图所示:

在埃博拉病毒爆发期间,感染人数持续上升,并且一年后,在缺乏有效药物的抵抗的情况下,感染病毒人数达到顶峰。在加入药物治疗对病情进行控制后,感染人数急剧降低,并在迭代22次后,感染元胞数量为零,即所有的感染患者都被治愈。而通过CA模拟药物的治疗效果,可以得到根除埃博拉的预计时间为3个月。(忘了咋算的了)
同时,在分析下埃博拉病毒的死亡率,定义的死亡率为:死亡元胞数量除以死亡元胞数量与感染元胞数量的和。
在埃博拉病毒爆发期间,死亡率呈上升趋势,但在加入药物对病情进行控制后,被感染元胞迅速被治愈,在迭代22次后死亡率迅速上升至100%,因为此时只含死亡元胞。感染元胞数量为零,即所有的感染患者都被治愈。
以红色代表感染状态,且颜色越深感染时间越长,灰色代表死亡状态,白色代表康复状态。下图描绘了加入药物治疗因素后,对埃博拉病毒的根除效果,感染人数(红色元胞)逐渐减少,逐渐转化为白色元胞,即被感染患者逐步开始被治疗。


灵敏性分析
人口流动
人口流动为传播埃博拉病毒的主要形式,当接触埃博拉病毒之后,随着人口流动,病毒也开始扩散,由最初的小村落传染至西非三个国家,甚至传播至欧洲、美洲,并且造成了破坏性影响。因此,我们讨论人口流动现象对疾病传播造成的影响。
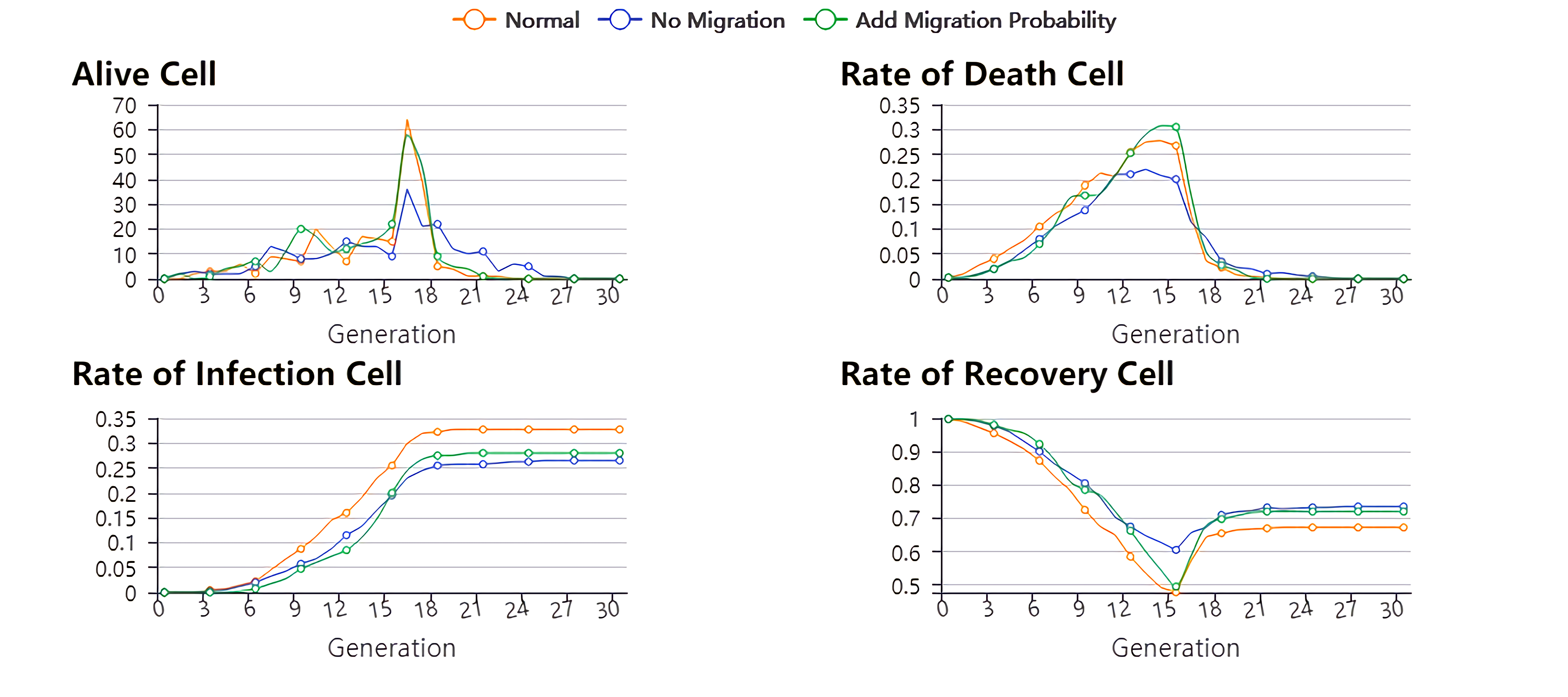
如图所示,当不存在人口流动现象时,元胞的存活率最高,即更少的人会被病毒感染,元胞的被感染几率最低,死亡率最低。而随着流动频率与流动范围的增加,元胞被感染几率上升,死亡率也上升。因此,人口流动现象影响了疾病传播情况,也影响了死亡率与感染率,因此,对于国家政府而言,应采取“戒严”形式,减少人口流动频率,对于减缓疾病传播与降低死亡率有着至关重要的作用。
加大治理力度
在以上灵敏性分析中,我们提出了国家应采取戒严措施防治疾病的进一步蔓延。而在其他方面,如提供充足的医疗设施;及时建立急救站点;发动较多医生甚至志愿者及时为患者提供的医疗服务,提高医疗效率,都能提高染病患者的存活几率。因此,我们讨论在加大疾病治理力度的情况下,对疫情的控制情况。
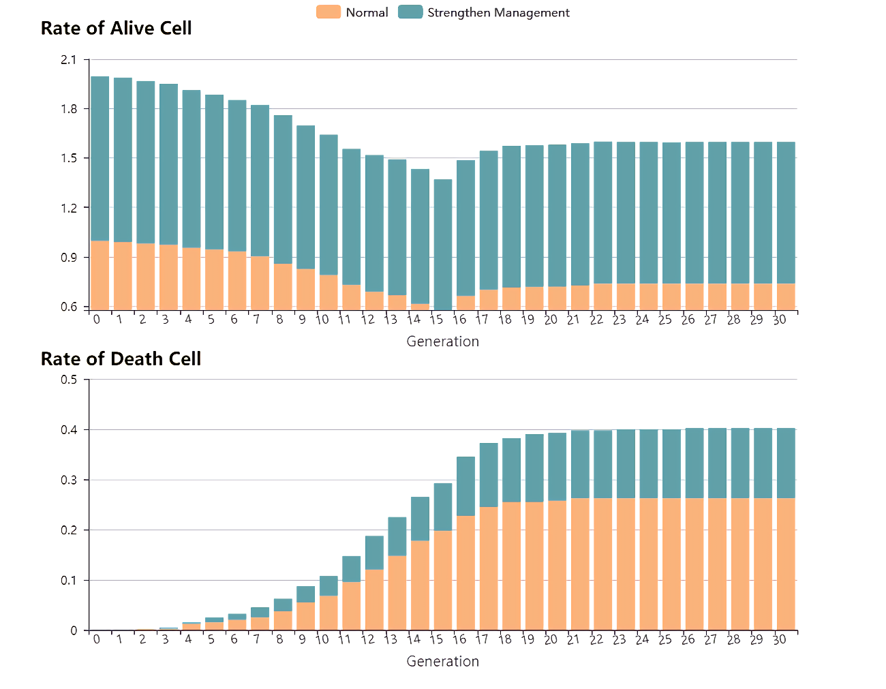
程序
下载,程序的原作者不是我,模型关系复杂到这里,这种难度的程序已经不是我这种技术渣可以写出来的了。
结语
针对埃博拉病毒传染问题,建立了符合题目要求的CA模型。充分考虑了感染率、死亡率、人口流动现象、治愈率等多方面因素,将这些因素影响融入CA中传播规则,模拟对疾病传播的影响,并与实际情况对比调整参数;在埃博拉病毒传播基础上,考虑药物治疗因素,重新定义CA传播规则,进一步模拟治疗效果。整体而言,准确模拟了疾病传播情况,并模拟药物治疗效果,预计根除艾比拉病毒所需时间,完成了工作。
并且在面临其他问题时,可对模型进行灵活的改动。根据需求重新定义传播规则,在改变元胞之间的联系规则后,可以模拟其他现象,并解决问题,具有很强的应用范围,如石油扩散、人口流动、交通运输等,因此,CA 模型具有很强的扩展性与灵活性。

