在之前的学习深度学习的过程中，以MLP为例，仅仅是知道了梯度下降和反向传播能很好的降低预测误差(本文暂且不谈论梯度消失和爆炸的问题)，使得训练出来的模型能够对未知的数据进行预测或者分类，以此来达到智能的目的。

时至今日，意识到不求甚解释不好的行为，于是下决心搞懂梯度下降和反向传播的原理。结果上网一搜，呵，大部分tm的是各处偷来的截图，截图里还有三四个水印，最后胡乱的堆一些数学公式，讲解的并不够彻底，也不通俗易懂。于是本文决定图解反向传播和梯度下降，并配备必要的数学计算，使读者一目了然。

基础知识

求偏导的概念得会一下(懂概念即可，不用自己求)，激活函数如何工作得会，网络的连接得会(搞明白参数在哪里工作就好了)。

梯度下降

我们先设一个简单的函数$y=3x^2+2x+1$。假设此时$x=10$，那么$y=321$，我们想优化这个函数，即利用梯度下降的方式来求得$y$的最小值和对应的$x$的值。~~为什么不求导直接算$y$的最小值？因为现实中的函数维度极度复杂，在复杂的函数空间内可能求不出来极小值点，这里只是用简单函数举例。~~可以求出目标函数的导函数为：$y’=6x+2$。万事具备，再来回顾下导数的意义~~非严谨数学定义，不要较真~~：

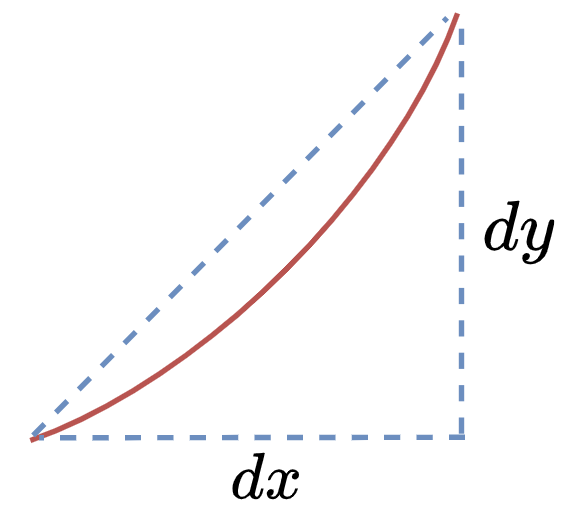
如上图所示，无限放大曲线的一小部分，在$y$轴方向截取一段$dy$，向$x$轴方向截取一段$dx$，则$f’(x)=dy/dx$即为这一小段曲线的斜率，也为导数值。当然，具体到实际问题，并不是取一段曲线而是以一个具体的点计算，这里只是距离。如$f(x)=2x^2$在$x=2$处的导数值为8。

梯度的本意是一个向量（矢量），即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大，显而易见，对一元函数而言就是求导(多元函数求偏导并含有方向)。继续推导，可以得到这样的式子：$f’(x)dx=dy$。在详细一点，当前$x=10$，我们取一个固定的$dx=0.2$，沿着导数的方向，让$x$逐渐的变化，此时的$y$也逐渐变小，是不是就能逐步得到目标函数的最小值呢？数学语言如下：

初始化$x$
开始迭代：
- 求$f(x)$的导数$f’(x)$
- $x_{i+1} = x_i - dx * f’(x)$
- $i ++$

即迭代示意图如下：

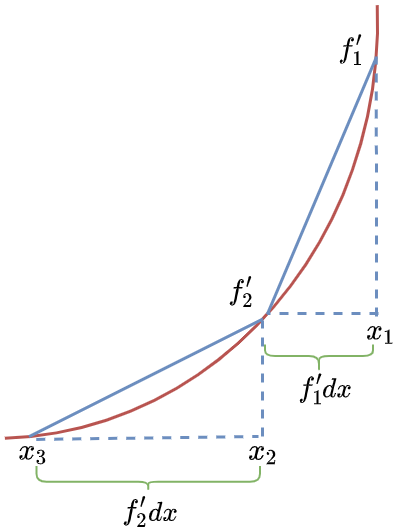
$x_1-f’_1dx=x_2$，$f’_1$为$x_1$处的导数值
$x_2-f’_2dx=x_3$，$f’_2$为$x_2$处的导数值

当然，$dx$也可以换成$\alpha$表示，含义为学习率，即每次行走的步幅。直到行走到最低点结束，代码如下：

dx = 0.2
n_eproch = 1000
x = -10 
ls = []

for _ in range(n_eproch):  
    y = 3 * x ** 2 + 2 * x + 1
    ls.append(y)
    x = x - (6 * x + 2) * dx

print(ls[-1])
# 0.67

可见在迭代1000次后，$y$的最终取值为0.67，和函数实际的最小值不谋而合~~利用中学知识求一下即可~~，这就是梯度下降的力量。当然，对于复杂的多元函数求偏导，或者求导的链式法则，还是借助Tensorflow这种专业工具更加省事。

import tensorflow as tf

X = tf.constant([0., 0.25, 0.5, 0.74, 1.])
y = tf.constant([0., 0.36, 0.54, 0.82, 1.])

a = tf.Variable(initial_value=0.)
b = tf.Variable(initial_value=0.)
variables = [a, b]

num_epoch = 100
optimizer = tf.keras.optimizers.SGD(learning_rate=5e-4)
for e in range(num_epoch):
    # 使用tf.GradientTape()记录损失函数的梯度信息
    with tf.GradientTape() as tape:
        y_pred = a * X + b
        loss = tf.reduce_sum(tf.square(y_pred - y))
    # TensorFlow自动计算损失函数关于自变量（模型参数）的梯度
    grads = tape.gradient(loss, variables)
    # TensorFlow自动根据梯度更新参数
    optimizer.apply_gradients(grads_and_vars=zip(grads, variables))

print(a, b)

反向传播

反向传播是一种以梯度下降为基础，对误差进行反馈，并调节相关参数的方法，因网络文章普遍都是公式较为晦涩，因此这里以数学计算为主，给出反向传播的实例，供读者理解。(因此期待看数学公式的可以移步了)。以MLP为例，首先构建结构如下图所示的网络：

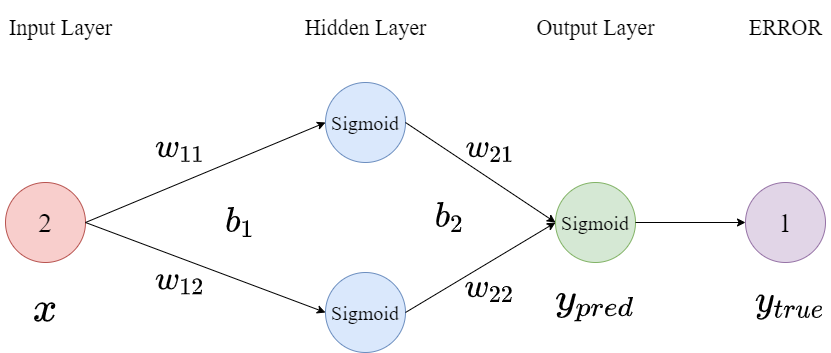
然后完成参数的初始化，且激活函数均采用Sigmoid($f(x)=\frac{1}{1 + e ^{-x}}$)

$x=2,w_{11}=1,w_{12}=-1,b_1=3,w_{21}=2,w{22}=1,b_2=0,y_{true}=1,\alpha=0.2$

前向计算

隐藏层第一个神经元：$x\times w_{11} + b_1 = 5$，激活后的输出为0.99
隐藏层第二个神经元：$x\times w_{12} + b_1 = 1$，激活后的输出为0.73
输出层的预测输出为：$y_{temp}=0.99\times w_{21} + 0.73\times w_{22} + b_2=2.71$，激活后的输出为0.93
计算Loss：$E=\frac{1}{2}(y_{true}-y_{pred})^2$ (选用这类型是是因为求导方便，绝对值函数不一定可导)

反向传播

补充一下对$\text{Sigmoid}$函数求导的结果为：$\frac{1}{1+e^{-x}}’=\frac{e^x}{e^{2x}+2e^x+1}$
$E$对输出层求导：$\frac{\partial E}{\partial y_{pred}}=y_{pred}-y_{true}=-0.07$
而$y_{pred}=\text{Sigmoid}(y_{temp})$，$\frac{\partial y_{pred}}{\partial y_{temp}}=\frac{e^{2.71}}{e^{5.42}+2e^{2.71}+1}=0.058$
而计算$y_{temp}$对$w_{21}$这个参数的偏导值：$\frac{y_{temp}}{w_{21}}=0.99$ (求偏导时无关变量视为常量)
通过链式法则求误差$E$对参数$w_{21}$的梯度：$\frac{\partial E}{\partial w_{21}}=\frac{\partial E}{\partial y_{pred}}\times \frac{\partial y_{pred}}{\partial y_{temp}} \times \frac{\partial y_{temp}}{\partial w_{21}}=-0.004$
$w_{21}$沿着梯度下降即可：$w_{21}=w_{21} + \alpha \times -0.004=2+0.2\times -0.004=1.9992$，这样，参数$w_{21}$就得到了更新。(同上文的梯度下降方法)

以此类推，通过不断的迭代，参数会逐渐修改，最终的结果是模型能有效的对输入进行预测或者分类。其他参数的更新同理。对于经常变成的小伙伴，会发现训练过程经常使用batch，此时最终的误差为这个bacth的总误差，需要对总误差求均值或求和等操作：

1 2	loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred) loss = tf.reduce_mean(loss)

结语

总算搞明白了梯度下降和反向传播的工作原理。其实，这么手推一下也就对梯度爆炸和梯度消失有了大概的了解。
学习率$\alpha$不是一成不变的，可以根据学习状态进行更新，参考这里：
https://muyuuuu.github.io/2019/02/20/gradient-function/
与大部分网文不同的是，本文尽力用通俗的语言讲解清楚了这两个东西，同时也会成为我的学习笔记。所以我没有给图片打水印的打算，只是受到网页浏览的限制，并没有上传高清图。如果你感觉本文还不错，且想分享，可以随意拷贝走本文的图片，嫌清晰度低可以在评论区找我要原图。
如果你对本文的某些细节描述还是不懂，可以评论区见，我也尽力做一个用大白话讲明白高深原理的人。

Just for Life.

图解反向传播与梯度下降

基础知识

梯度下降

反向传播

前向计算

反向传播

结语