弹性光网络选路和频谱分配问题建模

本博客来自于某课程的大作业。按照我之前建模的习惯，会直接『元胞自动机』设置规则直接模拟；但是却看到了通过优化来建立模型的做法。前者是基于规则的模拟，后者是凸规划问题下的求解。对于获得的解而言，在理论上还是后者更好一些，毕竟存在最优解。

问题描述

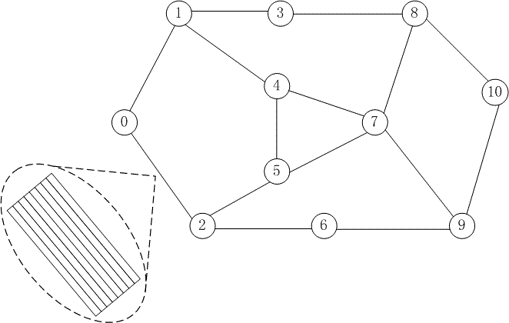
在上图中，一个网络中含有多个节点，如：交换机、路由等设备。当网络中的业务仅仅需要从各自源结点到达各自目的结点传输一定的数据时，利用这个网络就能实现数据传输的目的。该网络具有以下特性：

1. 网络节点之间有通信链路作为连接，称为边；
2. 网络中的每条边有多个频隙，每条边上频隙数目一样，且每个频隙具有相同的容量，即每条边传输的数据量是一样的；
3. 一个频隙在同一时刻只能在执行单个任务，即：结点2和结点5之间的边上的1,2,3号频隙有任务时，不能再将该频隙分配给其他业务；
4. 频隙连续且一致，即：
   1. 连续：数据包占用的频隙是相连的，是1,2,3这样的频隙，不能是1,3,4这样的频隙；
   2. 一致：数据包在第一条边上的频隙是1,2,3，经过节点转发，进入下一条边时，占用的频隙仍然是1,2,3。

当网络中有一批业务时，需要一个节点（源节点）向网络中的另一个节点（目的节点）传输一定量的数据（业务），我们需要做哪些工作？试建立数学模型解决此问题。

问题分析

建立的模型应至少解决以下两个问题：

1. 为每条业务选择一条路径；
2. 在每条路径中为任务分配频隙；

但需要在解决以上问题的基础上，需要达到占用带宽最小等目标，因此需要建立优化模型解决此问题。

符号说明

• $N$，网络中节点数量，节点编号为1到$N$
• $v_i$，网络中第$i$个节点$(1\leqslant i\leqslant N)$
• $E$，网络中边的集合
• $e_{ij}$，网络中起始点为$i$，目标点为$j$的边
• $F$，网络链路中频隙数量，频隙编号为1到$F$
• $M$，需要实现的任务数量
• $A$，业务请求集合：$\{A_1, A_2, \cdots, A_M\}$
• $A_k$，第$k$个业务，$A_k=\{s_k, t_k, b_k\},(1\leqslant k \leqslant M)$
• $s_k$，第$k$个业务的起始节点$(1\leqslant s_k \leqslant N)$
• $t_k$，第$k$个业务中的目的节点$(1\leqslant t_k \leqslant N)$
• $b_k$，第$k$个业务中需要占用的频隙数$(1\leqslant b_k \leqslant F)$

模型假设

考虑到理论模型与实际工程中存在的误差，基于以下假设来简化模型的建立：

1. 假设链路在多次使用和传输了大量数据后，链路并不会因老化而产生性能损耗。即频繁使用不影响链路的传输速率和传输量，传输速率和传输数据量始终保持恒定；
2. 假设按编号顺序依次分配任务所需占用的频隙，除保护频隙外无空余频隙。举例说明：当一条链路有10条频隙时，第一个任务占用5个频隙，则分配1-5号频隙，而不是3-7号等不按顺序编号的频隙；第二个任务也占用此条链路时，若其需要占用3条频隙，考虑到保护频隙，第二个任务将占用7-9号频隙，而不是选用8-10号等产生空余频隙的方案。

模型建立

优化目标

在光纤网实现传输数据的任务中，应从时间和成本两个方便考虑。以时间角度出发，应尽可能快的完成传输任务；从成本角度出发，使用的资源尽可能的少且均衡，即不能频繁使用一条链路，而其余链路一直处于空闲状态。而在本次建立的模型中，为简化优化目标的复杂性，将时间因素转换为约束条件，即尽可能的减少传输时间作为约束条件。

从成本角度出发，首先考虑尽可能减少使用带宽资源这一目标，以减少带宽的使用。以$F_{ij}$表示链路$e_{ij}$上被占用的最大频隙号。则此时的优化目标为：

\begin{equation}
\min\Bigl(\max_{e_{ij}\in E}(F_{ij})\Bigr)
\end{equation}

而在实际工程中频繁使用同一条链路，势必因负担过大而造成性能损耗。应均匀的使用所有链路，避免某些链路一直处于空闲状态。因此针对均衡使用链路资源这一目标，以$D_{ij}$表示起点为$i$，终点为$j$的链路$e_{ij}$的使用次数。计算所有链路使用次数的方差，使方差最小作为第二个优化目标：

\begin{equation}
\min\Bigl(\text{Var}_{(i,j)\in E}(D_{ij})\Bigr)
\end{equation}
其中，$\text{Var}$表示求方差。

如网络中有两组任务，第一组任务：从$v_i(1\leqslant i \leqslant N)$节点出发，到$v_j(1\leqslant j \leqslant N)$节点，需要占用路径中的全部频隙；第二组任务：仍然从$v_i(1\leqslant i \leqslant N)$节点出发，仍然到达$v_j(1\leqslant j \leqslant N)$节点，同样需要占中路径中的全部频隙。此时，两组任务的执行必须有先后的顺序关系。所以路径中涉及的链路必然会被多次使用，故第二个优化目标具有一定的合理性。综上所述，优化目标为：

\begin{equation}
\min\Bigl(\max_{e_{ij}\in E}(F_{ij})+\text{Var}_{(i,j)\in E}(D_{ij})\Bigr)
\end{equation}

约束条件

如果只是简单的设置节点之间的转发规则，当满足条件时转发数据。此类基于规则的贪心算法只能寻找到问题的可行解，甚至不是局部最优解，或容易陷入局部最优解而非全局最优解。因此，应该建立约束条件，在约束条件下借助优化算法寻找目标函数的优化解，如借助遗传算法、粒子群算法等。但需要注意的是，因为优化目标和约束条件本身具备的复杂性，此类算法不能保证一定能寻找到问题的最优解，求得的解往往是局部最优解。

根据问题描述，应考虑以下4个约束条件：

1. 起始节点和目标节点之间的路径是相通的；
2. 对于一个任务，要分配连续的频隙；
3. 一条链路中使用的频隙数要小于链路允许的最大频隙数；
4. 一个频隙在同一时刻只能执行一组任务，不能有多个任务同时使用一条频隙。

路径可行性约束

业务$A_k(\forall A_k\in A)$的起始节点和目标节点之间的路径应该是相通的。设$P_k=\{P_k^1, P_k^2, \cdots, P_k^{N_k}\}$为起始节点和目的节点之间可行的路径集合，$N_k$表示可行路径的数量。$x_k^q$为布尔变量，当选择第$q$条路径时，其值为1；若不选择第$q$条路径，$x_k^q$的取值为0，且只能选择一条路径。

考虑到应该尽可能快的完成传输任务，对于每一个任务$k$，即当源节点到目标节点有多条路径时，应选择传输速率最快的路径。综合考虑两者，列出约束条件：

\begin{equation}
\sum_{1=1}^{N_k}x_k^q=1,x_k^q=\min\{t(P_k^1), t(P_k^2), \cdots, t(P_k^{N_k})\},\forall A_k \in A
\label{time}
\end{equation}

其中，$t(P_k^i)$表示单位大小的数据在路径$P_k^i(1\leqslant i \leqslant N_k)$上传输的时间。

频隙连续性约束

设$f_k^q(ij)$为任务$A_k$在路径$Q_k^q$中的链路$e_{ij}$上可用的起始频隙编号，则$(1\leqslant f_k^q(ij) \leqslant F)$。若在此链路中分配该任务，应保证该任务占用的频隙号是连续的。因此，从$f_k^q(ij)$开始，按编号顺序连续分配其他频隙，应保证分配的频隙数和任务$A_k$需要的频隙数$b_k$相等。列出约束条件：

\begin{equation}
\sum_{p=f_k^q(ij)}^{f_k^q(ij)+b_k-1}H_{qp}=b_k,\forall e_{ij}\in Q_k^q
\end{equation}
其中，$H_{qj}$为布尔变量，取值为0或1。当路径$Q_k^q$中的频隙$p$被选择时，取值为1，否则取值为0，以此来满足分配的频隙数和所需的频隙数相等的约束。需要注意的是，路径$Q_k^q$中的所有链路$e_{ij}$应该均满足这一约束。

频隙数与任务不重叠约束

因为变量$f_k^q(ij)$表示路径$Q_k^q$允许任务$k$的起始频隙编号，所以并不会存在同一时刻一个频隙内有多个任务重叠的情况，如下图所示。在左图中，一条链路中共有$F$个频隙，一个任务已经占用了$n$个频隙。若之后的任务若使用此条链路，则允许的起始频隙号$f_k^q(ij)=n+1$。在右图中，若链路尚未被使用，则允许的起始频隙号$f_k^q(ij)=1$。

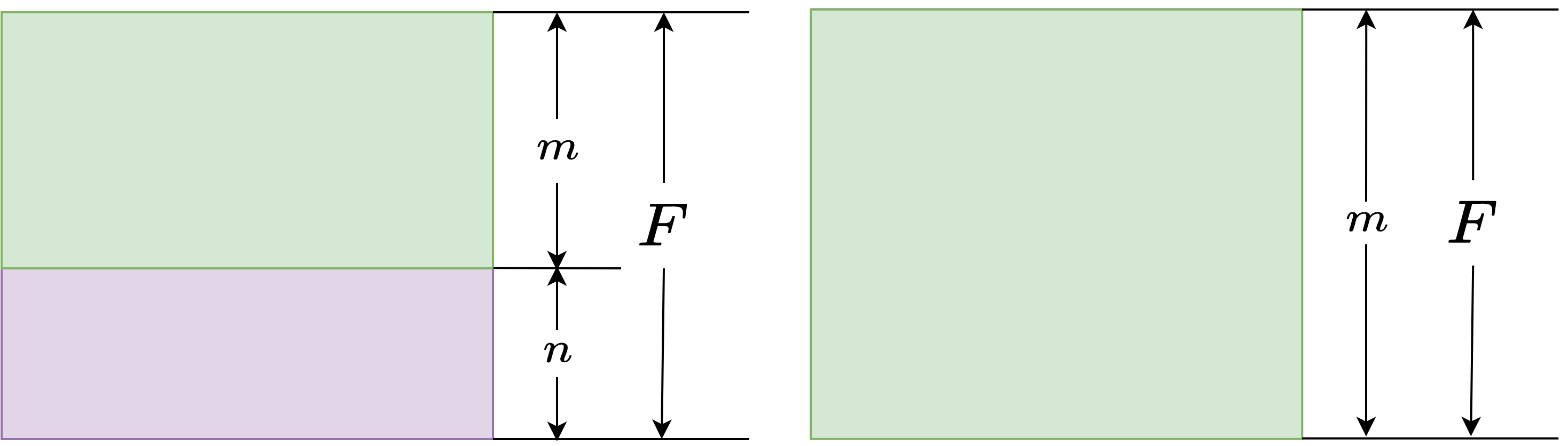
因此当有多个任务使用同一条链路时，对于之后进入的任务，允许使用的起始频隙号会自动增加，因此避免了同一时刻多任务重叠在一个频隙内的错误情况。但对于可行路径$Q_k^q$中的所有链路$e_{ij}$，要满足使用频隙数不小于最大频隙数的约束，列出约束条件：

\begin{equation}
f_k^q(ij)+b_k-1 \leqslant F, \forall A_k \in A, \forall e_{ij} \in E
\end{equation}

结论

因此，得到的最终优化模型为：
\begin{align}\notag
&\min\Bigl(\max_{e_{ij}\in E}(F_{ij})+\text{Var}_{(i,j)\in E}(D_{ij})\Bigr) \\
&\text{s.t.}\quad
\begin{cases}
\displaystyle{\sum_{1=1}^{N_k}x_k^q=1,x_k^q=\min\{t(P_k^1), t(P_k^2), \cdots, t(P_k^{N_k})\}}\\
\displaystyle{\sum_{p=f_k^q(ij)}^{f_k^q(ij)+b_k-1}H_{qp}=b_k,\forall e_{ij}\in Q_k^q} \\
\displaystyle{f_k^q(ij)+b_k-1 \leqslant F, \forall A_k \in A, \forall e_{ij} \in E}
\end{cases}
\end{align}

灵敏性分析

链路老化带来的问题

模型假设了链路在多次使用和传输大量数据后，链路并不会因老化而产生性能损耗，即在频繁使用的情况下，链路的传输速率和传输数据量始终保持恒定。但在实际工程的使用中，这一假设并不成立，链路会受到天气、人为、电磁场等影响，因而产生不可避免的老化与损耗。

假设某一时刻链路因老化，传输数据量受到影响，对比进行分析。举例说明：针对大小相同的数据量，新链路用5条频隙就能传输完毕，而老化的链路则需要8条链路来传输。此时，只需要对链路老化程度进行监测，或通过历史数据建立链路老化程度与链路使用次数$D_{ij}$的关系函数（$i$为一条链路的起点，$j$为一条链路的终点，$ij$相邻）。举例说明此关系函数的含义：当链路的使用次数达到$B$次后，需要增加$C$条频隙来传输单位大小的数据量。之后通过软件更改任务$A_k$中$b_k$的大小即可，例如将5改成8，而不需要修改建立的模型。

当链路的传输速率也受到影响时，会对路径可行性约束中的时间函数$t(x)$带来影响，从而影响最短路径的选择。同上需要建立传输单位数据的时间与链路使用次数$D_{ij}$的关系函数（$i$为一条链路的起点，$j$为一条链路的终点，$ij$相邻）。举例说明此关系函数的含义：当链路的使用次数达到$B$次后，传输单位大小数据量将减慢$g$倍。此时，因为速率减慢，在模型中的路径可行性约束中，公式\eqref{time}中路径$x_k^q$的选择将会受到影响。但只会影响路径选择的结果，而不用重新建立模型。

综上所述，在去除模型假设的情况下，建立的优化模型具有一定的稳定性。