之前了解到,可变形卷积 DCN(Deformable Convolutional Networks)是上分常用小技巧,所以把论文找来读了一下,V1 和 V2 两个版本都读了一下,个人感觉以及他人复现的结果显示 1 ,V1写的很好且够用,V2 写的实在是晕头转向。感觉还挺有创意,后期准备复现后,以后可能会用到。
概述
传统的 CNN 在建模时,几何变化能力受限,感受野都是规则的相邻矩形。于是,提出了可变形卷积,通过无监督的形式学习额外的偏移参数,加强模型的几何变换能力。也就是说,有了偏移参数,此时的卷积核读取的输入不再是规则的矩阵。且像传统 CNN 一样,支持端到端训练和反向传播,可以通过插拔的形式替换传统模型中的 CNN 。
- 偏移参数是在输入的特征图上增加额外的网络分支,自己学出来的,所以这是一种自适应的方式
- 在 ROI 时,也可以学习这种偏移参数,自适应的定位到感兴趣区域
- 两者都是通过添加额外的网络分支实现的,但计算量不大
其实这种形式挺重要的,尤其是算法部署到真实世界,是无法提前预知目标和图像的大小的。而如果模型有这种自适应感知目标区域大小和调节感受野的能力则再好不过。如下图所示,DCN 相比 CNN 而言,能更好的感知目标区域。

变形卷积算法
首先定义区域 $R$ 是输入特征图 $x$ 中的规则矩形,卷积核的权重是 $w$,区域 $R$ 中的元素的含义为横坐标的偏移与纵坐标的偏移量,所以可以通过 $R$ 了解到卷积核的大小和扩张大小。
\begin{equation}
R = \bigl( (-1, 1), (-1, 0), \cdots, (0,1), (1,1) \bigr)
\end{equation}
上面公式中,卷积核的大小就是 3,元素数量是 9,扩张大小为 1。以 $y$ 表示输出特征图,那么 $y$ 在 $p_0$ 位置的取值为 :
\begin{equation}
y(p_0) = \sum_{p_n \in R} w(p_n) x (p_0 + p_n)
\label{traditional}
\end{equation}
$(p_0 + p_n)$ 的意思是偏移到目标像素 $p_n$,原文没有解释,我看了半天才看懂。这也就是传统的卷积。如果我们对 $R$ 中的每一个位置的元素都有一个通过神经网络学习得来的偏移量 $(\Delta p_n | n=1,\cdots,N)$,那么公式 $\eqref{traditional}$ 可以改写为:
\begin{equation}
y(p_0) = \sum_{p_n \in R} w(p_n) x (p_0 + p_n + \Delta p_n)
\end{equation}
此时的卷积可视化如下图中的 b c d 部分,a 是标准的卷积。
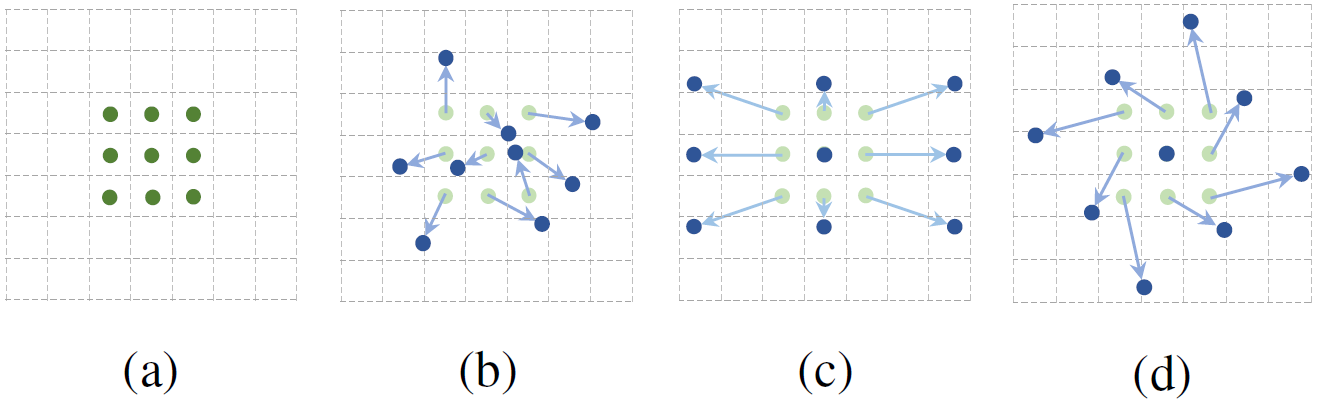
因为 $p_n + \Delta p_n$ 可能是一个小数,所以需要使用双线性插值来对坐标取整,用 $p$ 来表示 $p_0 + p_n + \Delta p_n$,公式如下:
\begin{equation}
x(p) = \sum_{q} G(q,p)x(q)
\end{equation}
$q$ 是输入特征图中的像素,其实只用到了和 $p$ 相邻的一部分。而 $G$ 是一个二维的双线性插值核函数,可以用两部分表示:
\begin{equation}
G(q,p) = g(q_x,p_x) \cdot g(q_y,p_y)
\end{equation}
其中,$g(a,b) = \max(0, 1- |a-b|)$,所以这里也能看出来,如果 $a,b$ 相差很大,取值会为 0,所以每次计算取 $q$ 时,其实只用到了和 $p$ 相邻的一部分。
变形卷积训练流程
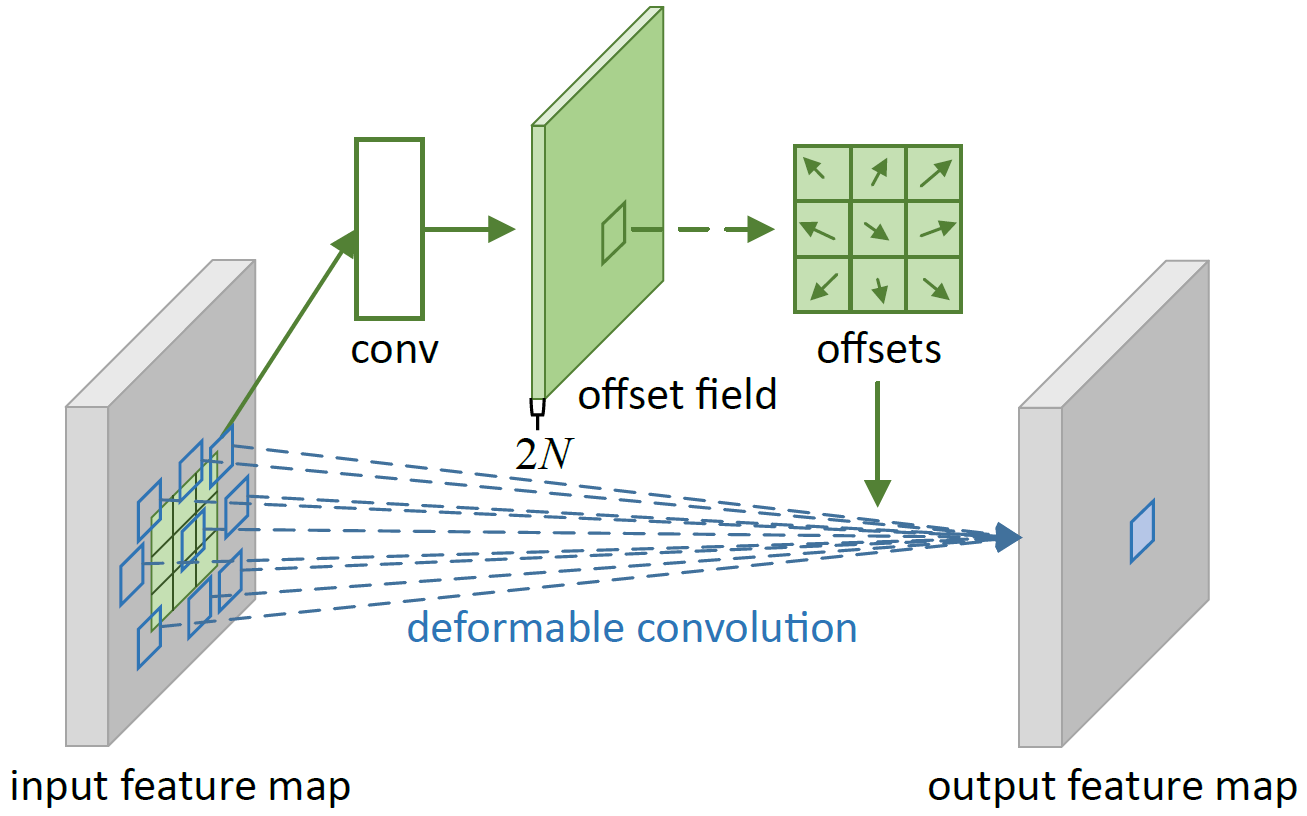
如上图所示,假设 $R$ 中卷积核的元素数量是 $N$,比如 $3\times 3$ 卷积核的元素数量就是 9。那么就增加一个旁路卷积,这个卷积的通道数就是 $2N$,且卷积前后尺寸不变。这样做的原因是,计算 $x$ 方向和 $y$ 方向共两个方向的偏移量。取前两个通道,就是当前卷积核处理像素点的横坐标偏移和纵坐标偏移。
变形 ROI Pooling
其实道理也和上面一样了,假设此时在目标检测中将特征图 ROI pool 到 $k\times k$ 的矩阵中,以平均池化为例,输出 $y$ 中第 $(i,j)$ 个元素的取值就是
\begin{equation}
y(i,j)=\sum_{p\in bin(i,j)} x(p + p_0) / n_{ij}
\end{equation}
$bin$ 表示要被池化的区域,$n_{ij}$ 是对应区域中的像素点的数量。而此时,可以学习一个偏移量参数 $\Delta p_{ij}$,新的 ROI Pooling 公式就是
\begin{equation}
y(i,j)=\sum_{p\in bin(i,j)} x(p + p_0 + \Delta p_{ij}) / n_{ij}
\end{equation}
双线性取整部分就和之前的一样了。不过论文中注明了一点,网络学习到的是 $\Delta \hat{p}_{ij}$,如下图所示,使用全连接计算每个像素点的偏移量。
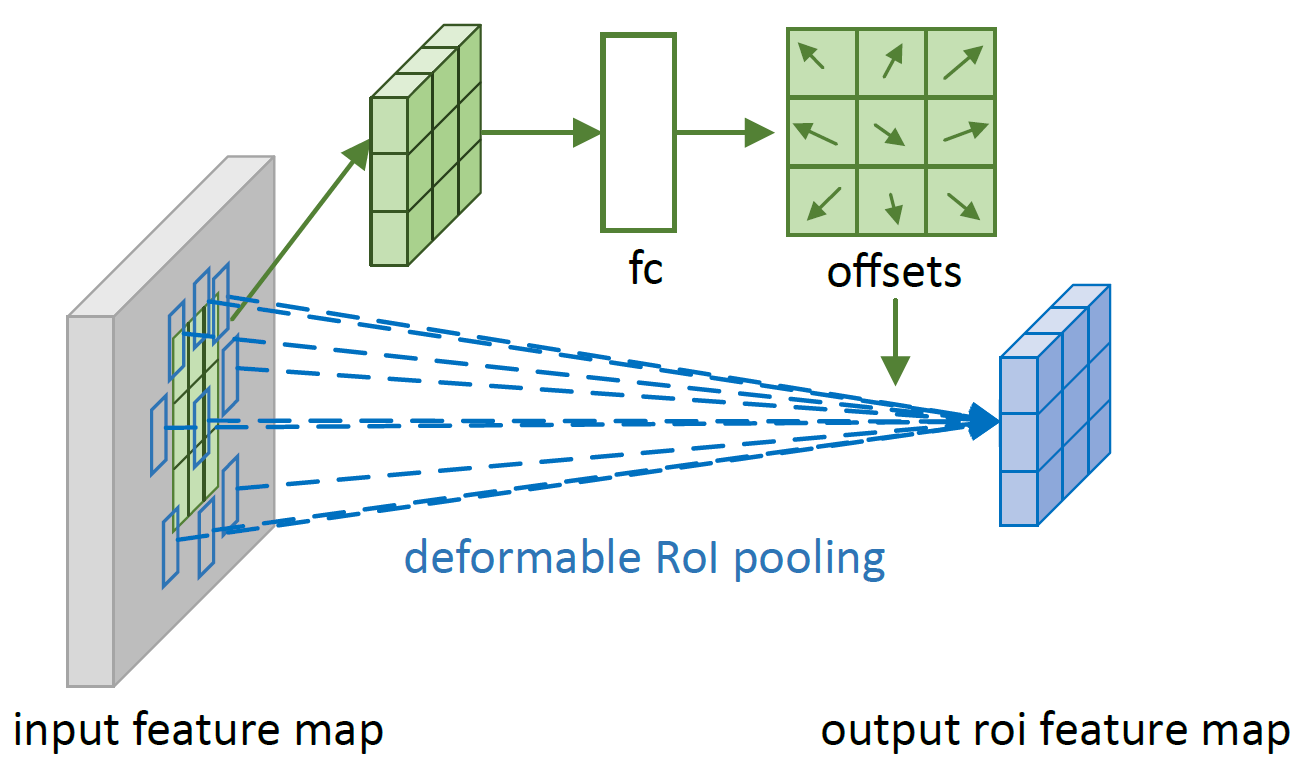
而 $\Delta p_{ij} = \gamma \cdot \Delta \hat{p}_{ij} \circ (w,h)$,$\gamma$ 的取值是 0.1,$(w,h)$ 是 ROI Pooling 之前的特征图的宽度和高度,$\circ$ 运算是什么,文中没有声明。
V2
DCN V2 看的我属实头晕,不过大体贡献还是能看清的,集中改进了两点:
- 采样时,如果采到了背景区域,会对目标分类与检测造成影响,所以要抑制背景区域的贡献
- 训练一个教师网络,类似判别器,用于指导检测网络的检测,文中称为特征模仿(feature mimicking),没读懂这个和前文改进的联系,唯一的相似点是摘要中指出的:提高模型捕获特征的能力,但我感觉这里是重点
以可变形卷积为例,原有 DCN 的输出通道是 $2N$,那么作者将输出通道改为 $2N+1$,最后一个维度用 sigmoid 激活到 (0, 1) ,表示为符号 $\Delta m_k$ ,含义为当前像素点的贡献程度,如果是背景噪音,那么贡献会趋于 0。所以此时可变形卷积的公式为:
\begin{equation}
y(p_0) = \sum_{p_n \in R} w(p_n) x (p_0 + p_n + \Delta p_n) \cdot \Delta m_k
\end{equation}
至于 ROI Pooling 也是一个道理了。
特征模仿
而另一个创新点是特征模仿,在主干网络 RPN 后,将得到的题夷旷送到另一个 RCNN 分支,两个分支的输出的相似性做对比作为损失,相似度越高,损失越小,相似度越低,损失越大。相似度是用 $\cos$ 函数计算的。
- 测试时,不适用右侧的 RCNN分支
- 两个分支的 bacbone 部分共享参数
- 三个损失一起反向传播
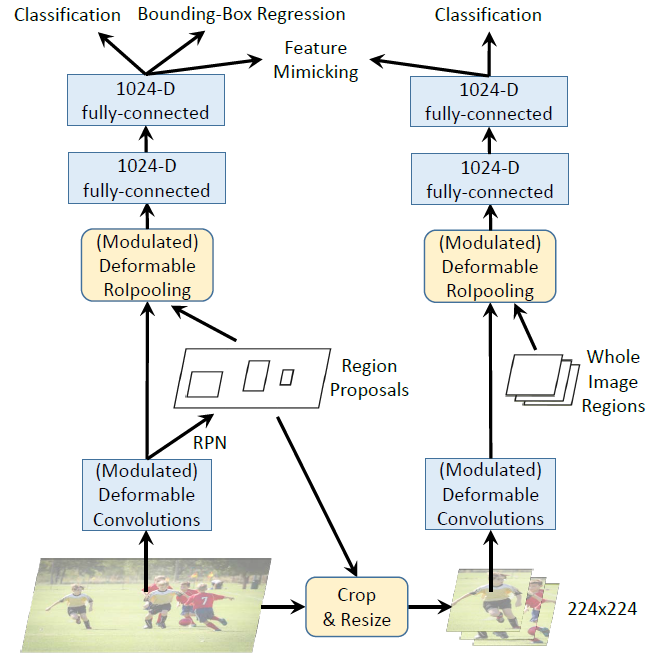
reference
- 1.https://github.com/open-mmlab/mmdetection/tree/master/configs/dcn ↩

