论文好像是 2020 年底传到 arxiv 1 的,还比较新。正好最近遇到的问题是类别数量是长尾分布,恰好最近看到 mmdetection 也支持了这个损失函数,索性来看一看这篇论文,算是做个论文笔记吧。不过为了能更容易理解论文的思想,没有按照原论文的内容结构进行整理。
概要
在现实世界中,只有少部分类有充足的数据,大部分类别其实只有小部分数据,这就是类别数量呈现长尾分布。如下图 2 所示:
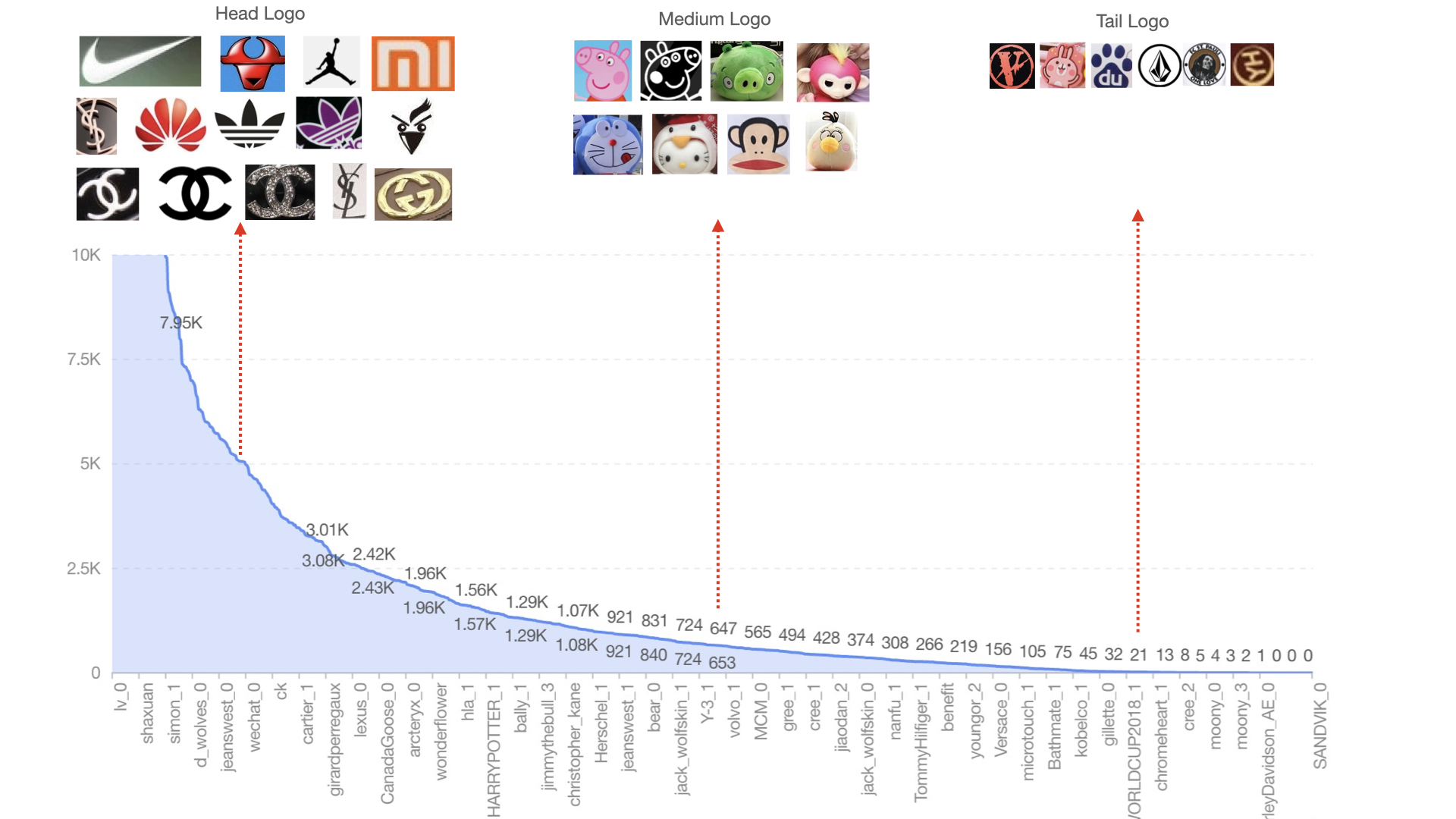
而头部类实例在长尾数据集中占主导地位,这些实例为尾部类提供了大量的负样本。所以正样本和负样本在尾类上的梯度严重不平衡。说人话的意思是,含有尾部类别的样本本是正样本,头部类别的样本是负样本。由于负样本的数量大于正样本,所以负样本对尾部类别的影响大于正样本对尾部类别的影响,具体为啥可以看公式 $\eqref{why}$。由于交叉熵公式的原因,负样本的梯度在学习过程中起到了决定性影响,导致尾部类别被识别为背景或头部类别。如下图所示:
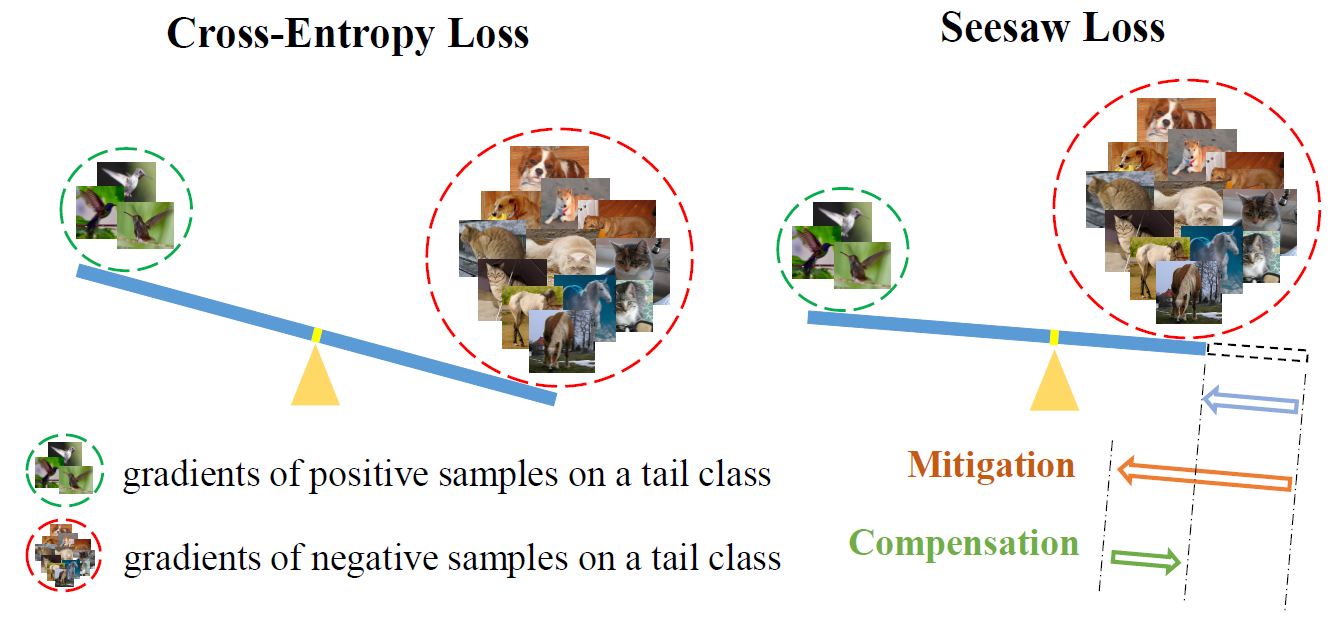
- 那些鸟明明是正样本,但目标小,类别少,导致不如右侧常见的负样本的梯度大。负样本梯度指:就是负样本对当前类别的惩罚。
以传统的交叉熵损失函数为例:
\begin{equation}
L(z) = -\sum_{i=1}^C y_i \log(\sigma_i), \sigma_i = \frac{e^{z_i}}{\sum_{j=1}^Ce^{z_j}}
\end{equation}
$z$ 表示为网络的逻辑预测输出,$\sigma$ 表示网络对每个类别的预测概率。如果当前类别是 $i$,那么对 $z_i$ 和 $z_j$ 的梯度为:
\begin{equation}\label{why}
\frac{\partial L}{\partial z_i} = \sigma_i - 1, \frac{\partial L}{\partial z_j} = \sigma_j
\end{equation}
上述公式中可以看到,第 $i$ 类样本在分类时,也惩罚了类别 $j$,换句话说,类别 $j$ 的输出单元也要受到影响。如果类别 $i$ 是头部类别,类别 $j$ 是尾部类别,那么类别 $j$ 的输出单元、backbone 等网络参数将会在大多数样本中会受到惩罚,于是类别 $j$ 的预测就会受到抑制,导致上图所示的结果。务必看懂这一步,这也是论文要改进的点。
现有的一些处理长尾分布的做法是(这部分就是 related works 抄来的,我没看里面的论文):
- 根据不同的类别统计,调整损失来重新计算权重
- 重采样技术,保证类别平衡
- 在预训练的模型上,用类平衡技术重新训练分类头
- 对不同的类别使用不同的分类器去预测
算法
创新点
- 对于每一个类别,通过缓解(mitigation)因子 $M_{ij}$ 和补偿(compensation)因子 $C_{ij}$ 动态的重新平衡正负样本的梯度
- $M_{ij}$ 在累积的训练过程中,在不同类别之间,减少对尾部类别的惩罚。
- 但是只减轻惩罚是不够的,因为其他类别的样本在被误分类为尾类时,尾部类别受到的惩罚仍然较小。说人话的意思是,类别 $j$ 相关的神经元受到的惩罚小,神经网络为了最小化损失,所以不管输入的是什么类,有可能直接输出第 $j$ 类,所以盲目地降低负样本的梯度会增加导致尾类假阳性的风险。所以增加 $C_{ij}$ 增加对错分类实例的惩罚,避免假阳性的出现,算是一种补偿机制。
所以 seesaw loss 有以下优点:
- 是动态的,它可以汇总全部训练集的信息,知道哪些是尾类,哪些被错分类,能够更好的调整损失
- 是自校准的,因为 $M_{ij}$ 和 $C_{ij}$ 能避免尾部类别被过度惩罚和假阳性
- 能更好的处理未知分布的数据集,毕竟在训练期间会统计各个类别的数目,所以能获得更好的正负样本梯度平衡
算法流程
文中定义的 seesaw loss 是:
\begin{equation}
L(z) = -\sum_{i=1}^C y_i \log(\hat{\sigma_i}), \hat{\sigma_i} = \frac{e^{z_i}}{\sum_{j\neq i}^CS_{ij}e^{z_j}+e^{z_i}}
\end{equation}
所以对 $z_j$ 的偏导数就是:
\begin{equation}
\frac{\partial L}{\partial z_j} = S_{ij} \frac{e^z_j}{e^z_i} \hat{\sigma_i}, S_{ij} = M_{ij} \cdot C_{ij}
\end{equation}
$S_{ij}$ 表示一种可调节的因子,表示类别为 $i$ 的正样本对类别 $j$ 的惩罚。其中,$M_{ij}$ 表示头部类别 $i$ 降低对尾部类别 $j$ 的惩罚,$C_{ij}$ 表示增加对类别 $j$ 的惩罚,当类别 $i$ 被误分类为 $j$ 时。
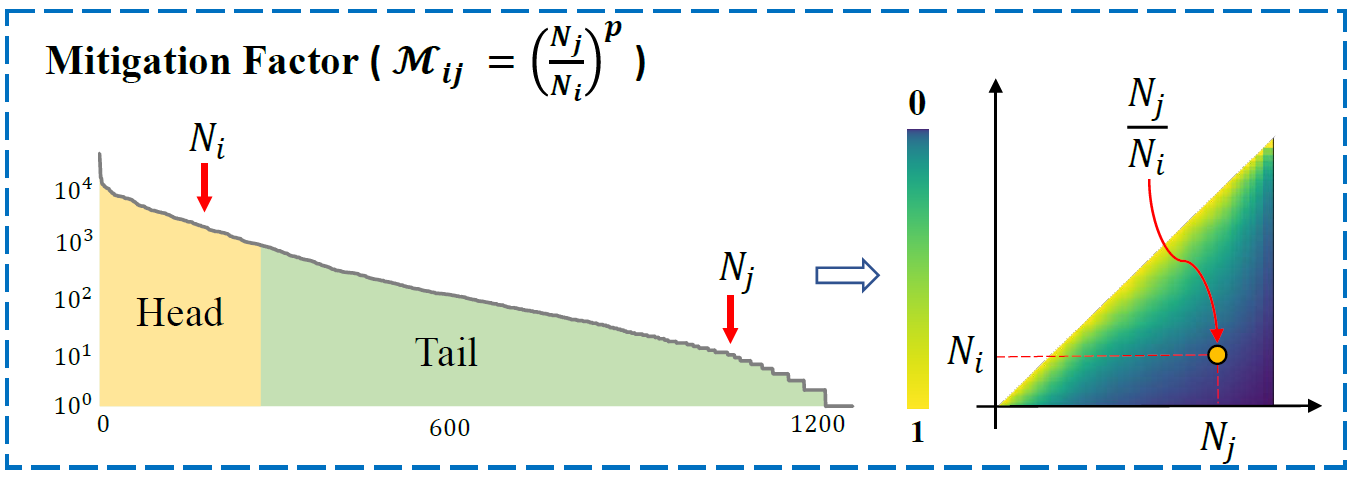
缓和因子
seesaw loss 在训练期间,会统计类别 $i$ 的数量为 $N_i$,对于正样本,也就是当前网络正在处理的类别 $i$,通过缓解因子调整对其它类别的惩罚,公式如下:
\begin{equation}
M_{ij} =
\begin{cases}
1, & N_i \leq N_j \\\\
\biggl(\frac{N_j}{N_i}\biggr)^p, & N_i > N_j
\end{cases}
\end{equation}
如上述公式,当类别 $i$ 的数量 $N_i$ 远远大于其它类别时,对其它类别的惩罚力度会降低。$p$ 是控制惩罚程度的超参数。需要注意的是,seesaw loss 会在训练期间统计类别数量,而不是事先统计。这样做有两个好处:
- 能适应不可见数据集,如训练数据来自流数据
- 每个类别的训练样本能被其它类别的数据适度的影响,更加鲁棒。比如当前每个类只有 5 个数据,就算不上谁是尾部,谁是头部,惩罚力度可以都一样,能更加均匀的初始化和光滑的适应真实世界的数据
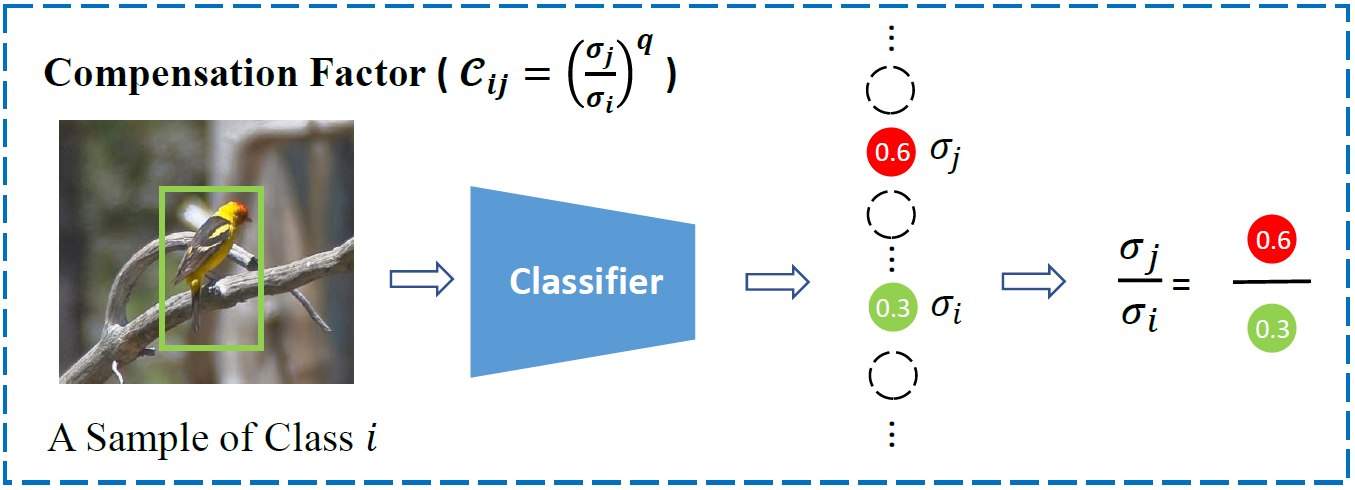
补偿因子
这个计算就和上面的公式类似了,假设当前类别是 $i$ 时,被误分类为 $j$,那么缓和因子的计算公式为:
\begin{equation}
C_{ij} =
\begin{cases}
1, & \sigma_j \leq \sigma_j \\\\
\biggl(\frac{\sigma_j}{\sigma_i}\biggr)^q, & \sigma_j > \sigma_i
\end{cases}
\end{equation}
$q$ 仍然是控制惩罚程度的超参数,被误分类的程度越大,补偿惩罚的力度就越大。
标准化线性层与输入
- 对于头部类别 $i$,与其相关的分类参数 $W_i$ 可能会比较大,抑制了其它类别的表达,所以对分类层进行 $L_2$ 正则化处理
- 输入也要做正则化处理,我好奇为啥不是标准化
注意事项
不知道读到现在有没有发现论文的一个明显漏洞。在目标检测领域,从候选框到 ROI Pooling,到处都有背景类的存在,所以背景类会是头部类别,且数量远远大于其它类,对其它类产生抑制。所以,seesaw loss 会减少对所有前景类的抑制,但由于采样问题,背景类数量几乎不会低于前景类,所以不会有对前景类的补偿因子,这样,可能会将背景识别为前景。
所以论文的想法是,增加一个前景背景的二分类器,预测目标属于前景的概率 $\sigma_i^{obj}$ 还是背景的概率,背景会被抛弃,前景会被保留。而预测阶段,会保留这个二分类器。最终预测的目标概率就是:
\begin{equation}
\sigma_i = \sigma_i^{obj} \cdot \sigma_i^{class}
\end{equation}
其它
这篇论文的想法讲真还是不错的。忙猜一下,会有论文说这篇论文的 $p,q$ 是手工设定的不太好,$M_{ij}$ 和 $C_{ij}$ 直接相乘不太好没有道理。然后写篇论文,用神经网络自适应的学习参数 $p,q$ 或 $M_{ij}$,然后说这是改进,性能好了一些。这样的东西我见过太多了,没意思,不过都是为了混一碗饭。

