在多年前的某次任务中，看到了别人使用提升树等算法，取得了比较好的效果。今日眼馋，特来学习提升方法，并记录于此。提升方法是一种统计学习方法。在分类问题中，通过改变训练样本的权重，学习多个分类器，将多个分类器进行线性组合，以提升分类的性能。

本文收录：

具有代表性的提升方法：AdaBoost算法；
算法原理
算法推导
算法解释
举例说明
代码实现

算法原理

提升算法的思想很简单：对于一个分类任务，一个专家说的结果可能不太可靠，但一群专家说的结果总是大体可靠的。即：多个专家说的话比一个专家说的话可信，多个分类器共同分类的结果要好于一个分类器分类的结果。

而训练一个弱分类器总比训练一个强分类器方便的多。那么针对一个训练集，提升方法就是先学习一个弱分类器，从弱分类器出发，改变训练数据的权重，反复学习到一系列的弱分类器，将这些弱分类器组合成一个强分类器。

这样，就导出了两个问题：

反复训练时如何更新数据的权重；
如何将多个弱分类器组成一个强分类器；

对于第一个问题：提高被前一轮分类器分类错误样本的权重，这样这些样本会在下一轮的弱分类器中受到更大的关注，于是分类问题将被一系列的弱分类器分而治之。

对于第二个问题：AdaBoost采用了加权多数表决的方法，即：加大分类误差率小的分类器的权重，降低分类误差率大的分类器的权重。使正确率高的分类器在表决的过程中起到更加关键的作用。

算法推导

输入：训练数据集$T\{(x_1, y_1), (x_n, y_n), \cdots ,(x_n, y_n)\}$，假设为二分类任务，标签为$\{-1, +1\}$。输出：最终的分类器 $G(x)$。

初始换训练数据的权重，均匀分布权重。 $D=(w_{11}, w_{1i}, \cdots, w_{1n}), w_{1i}=1/N,i=1, 2, ..., N$
设有$M$个弱分类器，对于$m=1, 2, …, M$：
使用权重 $D_m$ 的分类器训练数据，得到基本分类器 $G_m$
计算$G_m$ 在训练数据集合中的误差，误差率是分类错误样本的权重和。 $e_m=\sum_{i=1}^nP(G_m(x_i)\neq y_i)=\sum_{G_m{x_i}\neq y_i} w_{mi}$
计算$G_m(x)$这个分类器的权重：$\alpha_m=\frac{1}{2}\log \frac{1-e_m}{e_m}$，不难得到$\log \frac{1-x}{x}$为减函数，误差越小，权重越大
更新数据集的权重分布，有点softmax的意思，确定所有样本的权重和为1且为正数：
$D_{m+1}=(w_{m+1, 1}, w_{m+1, i}, \cdots, w_{m+1, N})$ $w_{m+1, i}=\frac{w_{m, i}}{Z_m}\exp (-\alpha_m y_i G_m(x_i))$ $Z_m=\sum_{i=1}^Nw_{m, i}\exp (-\alpha_m y_i G_m(x_i))$
当分类正确时，$y_i G_m(x_i)$同号，权重被减小；当分类错误时，权重放大，受到下一轮分类器的关注。
构建线性组合器：$f(x)=\sum_{i=1}^N\alpha_mG_m(x)$
得到最终分类器：$G(x)=\text{sign}(f(x))$，结果由$M$个分类器加权表决。

算法解释

其实，AdaBoost本质上为一种前向加法模型。即每次只优化当前的一步，后一步根据前一步的结果继续优化，得到最终的分类器。

前向分布算法

考虑加法模型

$\begin{equation} f(x)=\sum_{m=1}^M\beta_mb(x;\theta_m) \end{equation}$

$b(x;\theta_m)$为基函数，$\theta_m$为函数的参数，$\beta_m$为基函数的权重。在给定训练数据和损失函数的条件下，学习加法模型$f(x)$成为损失函数极小化的问题：

$\begin{equation} \min_{\beta_m, \theta_m}\sum_{i=1}^N(y_i, \sum_{m=1}^M\beta_mb(x;\theta_m)) \end{equation}$

这是一个复杂的优化问题，前向步算法求解此类问题的思路是：每一次只优化一个基函数和系数，逐步逼近优化目标，那么就可以简化优化的复杂度。因此每一步的极小化损失函数为：

$\begin{equation} (\beta_m, \theta_m)=\text{argmin}_{\beta_m, \theta_m}\sum_{i=1}^NL(y_i, f_{m-1}(x_i)+\beta_{m-1}b(x_i;\theta_{m-1})) \end{equation}$

得到新的参数$\theta_m, \beta_m$，更新当前加法模型为

$\begin{equation} f_m(x)=f_{m-1}(x)+\beta_mb(x;\theta_m) \end{equation}$

得到最终的加法模型：

$\begin{equation} f(x)=f_M(x)=\sum_{m=1}^M\beta_mb(x;\theta_m) \end{equation}$

举例说明

也许你公式看的很枯燥，但看个例子也就明白了，训练数据如下。目标是训练三个分类器：

$x$	0	1	2	3	4	5	6	7	8	9
$y$	1	1	1	-1	-1	-1	1	1	1	-1

第一个分类器：初始化每个样本的权重为0.1，分类误差率最低时，阈值$v_1=2.5$。得到的分类器为：当$x>2.5$时，$y=-1$，当$x<2.5$时，$y=1$，类似一个深度与1的决策树。计算得到误差率$e_1=0.3$，跟新第一个分类器的权重$\alpha$为$\frac{1}{2}\log\frac{1-0.3}{0.3}=0.4$，更新权重分布$D_1$（太长了就不一一列举了）。
第二个分类器：利用第一轮的权重结果$D_1$，更新数据集。此时分类错误率最低时，阈值$v_2=8.5$，且$x$小于8.5时判断为1。计算误差$e_2$，计算第二个分类器的权重$\alpha_2$，计算第三轮数据的权重$D_2$。因要求是训练三个分类器，这也是最后一次更新权重。
第三个分类器：按照第二轮的权重$D_2$，再次训练，分类错误率最低时的阈值为$v_3=5.5$，且$x$大于5.5时判断为1。而后计算误差，计算第三个分类器的权重。

也许你会问为什么有的时候大于有的时候小于？脑补决策树，具体是大于还是小于不是固定的。

三轮过后，得到的分类器为：

$\begin{equation} G(x)=\text{sign}[f_3(x)]=\text{sign}[0.4236G_1(x)+0.6496G_2(x)+0.7514G_3(x)] \end{equation}$

假设，输入的$x$为8，$x>v_1$第一个分类器$G_1(x)$的判断结果为-1，同理，第二个分类器的判断结果为1，第三个分类器的判断结果为1。带入$G(x)$，得到$-0.4236+0.6496+0.7514=0.97$，经过$\text{sign}$函数后取值为1，分到1那一类，且分类正确。

代码实现

终于到了激动人心的代码实现了，只是简单的完成二分类任务，借助sklearn实现。

首先通过sklearn创建训练数据；
其次设置不同的分类器的数量，观察分类的准确性；
打印分类器的误差和权重；
记录训练时间；
我看了源代码，样本权重封装的很好，想调出来不是很容易，就不调了；
绘制图像：随着分类器数量的增加误差逐渐减小；
更多操作请参考sklearn的官网，解释都挺详细的。

baseline 版本

from sklearn.ensemble import AdaBoostClassifier
from sklearn.datasets import make_hastie_10_2
import time

# 创建8000数据 4个特征 2个类
X, Y = make_hastie_10_2(n_samples=12000, random_state=1)

n_split = 2000

# 分类器的个数
num_estimators = [1, 5, 20, 50, 100, 200]

X_train, X_test = X[n_split:], X[:n_split]
Y_train, Y_test = Y[n_split:], Y[:n_split]

for num in num_estimators:
    clf = AdaBoostClassifier(n_estimators=num,
                             random_state=0,
                             algorithm='SAMME')
    
    # 记录算法的训练时间
    start = time.time()
    clf.fit(X_train, Y_train)
    end = time.time()

    score = clf.score(X_train, Y_train)

    print('Estimators ===>', num, ' Accuracy ===>', score, 'Time ===>', round(end - start, 2), 's')

    if (num == 5):
        print('Errors ', clf.estimator_errors_)
        print('Weights ', clf.estimator_weights_)
        print(clf.base_estimator_)

输出结果如下：

Estimators ===> 1  Accuracy ===> 0.5513 Time ===> 0.01 s
Estimators ===> 5  Accuracy ===> 0.6194 Time ===> 0.06 s
Estimators ===> 20  Accuracy ===> 0.7108 Time ===> 0.23 s
Estimators ===> 50  Accuracy ===> 0.8166 Time ===> 0.55 s
Estimators ===> 100  Accuracy ===> 0.8614 Time ===> 1.1 s
Estimators ===> 200  Accuracy ===> 0.8871 Time ===> 2.23 s

可见，对于较多的分类器，准确性有所提升。且，能在很短的时间内执行处不错的分类结果。当只有5个分类器时，我们打印一下每个分类器的误差和权重，并打印当前分类器，即选择了什么分类器。输出如下：

Errors  [0.4487     0.46195913 0.45847958 0.46397641 0.45167916]
Weights  [0.20592461 0.15245809 0.16646502 0.14434448 0.19388849]
DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=1, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

由上不难看出选择的分类器为：深度为一的选用基尼系数进行决策的决策树。

决策树版本

既然选用了决策树，何不增加一下决策树的深度？以此来提高分类的准确性。代码如下：

import numpy as np
import matplotlib.pyplot as plt
import time
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_hastie_10_2

# Construct dataset
# 创建8000数据 4个特征 2个类
X, Y = make_hastie_10_2(n_samples=12000, random_state=1)

n_split = 2000

# 分类器的个数
num_estimators = [1, 5, 20, 50, 100]

X_train, X_test = X[n_split:], X[:n_split]
Y_train, Y_test = Y[n_split:], Y[:n_split]

for num in num_estimators:
    # Create and fit an AdaBoosted decision tree
    bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=4),
                            algorithm="SAMME",
                            n_estimators=num)
    
    # 记录算法的训练时间
    start = time.time()
    bdt.fit(X_train, Y_train)
    end = time.time()

    score = bdt.score(X_test, Y_test)

    print('Estimators ===>', num, ' Accuracy ===>', score, 'Time ===>', round(end - start, 2), 's')

print(bdt.base_estimator_)

输出如下：

Estimators ===> 1  Accuracy ===> 0.6295 Time ===> 0.03 s
Estimators ===> 5  Accuracy ===> 0.741 Time ===> 0.2 s
Estimators ===> 20  Accuracy ===> 0.841 Time ===> 0.77 s
Estimators ===> 50  Accuracy ===> 0.9105 Time ===> 1.92 s
Estimators ===> 100  Accuracy ===> 0.937 Time ===> 3.86 s
DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=4, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

可见，在增加决策树深度后，准确性有了明显提升。

误差分析

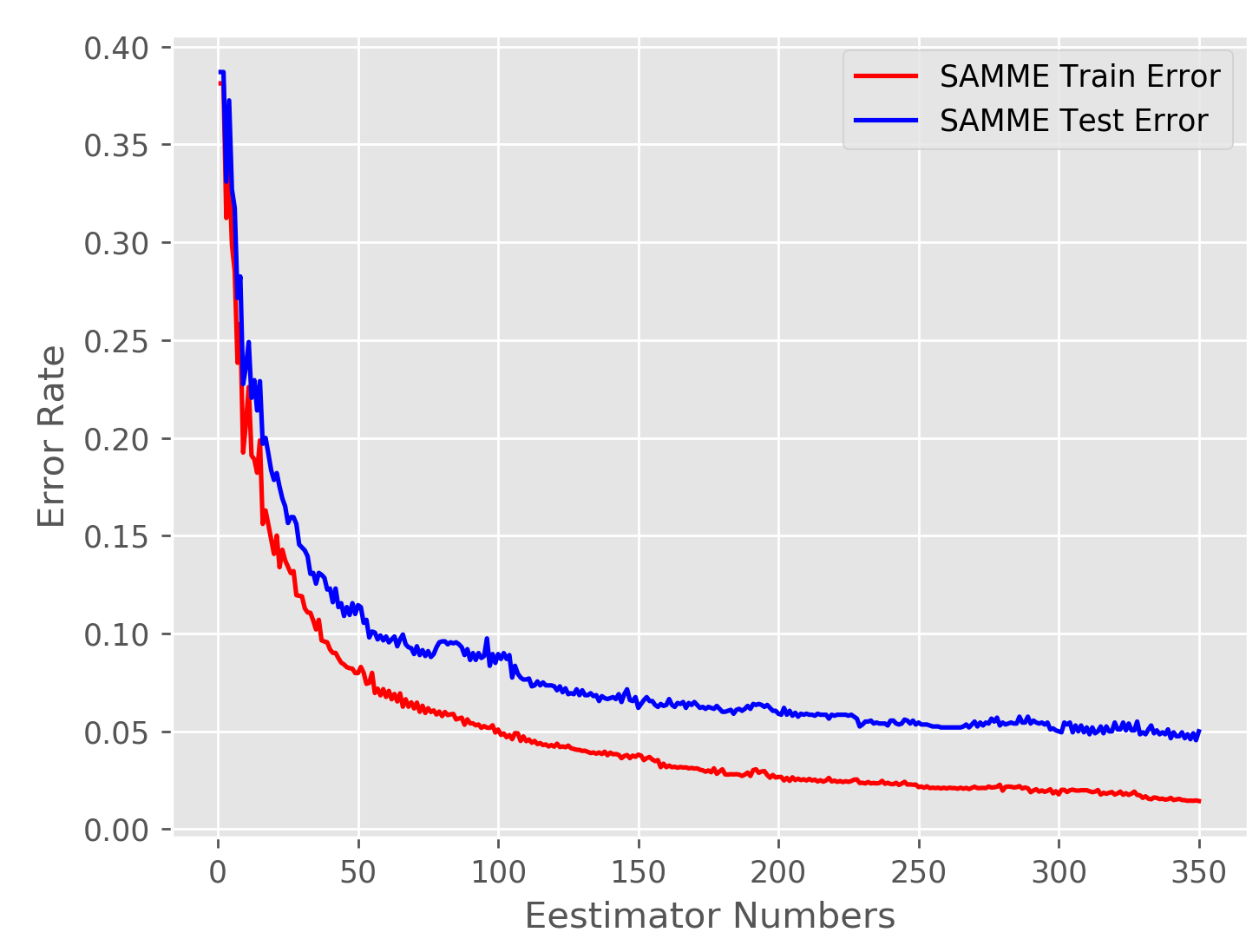
如图所示，随着分类器数量的增加，误差率逐渐下降并稳定在一个区间内。因为提升算法是有训练误差的界限的，其训练误差为：

$\begin{equation} \frac{1}{N}\sum_{i=1}^NI(G(x_i) != y_i) \leq \frac{1}{N}\sum_{i=1}\exp (-y_iG(x_i)) = \frac{1}{N}\sum_{i=1}\exp(-\sum_{m=1}^M\alpha_my_iG_m(x_i)) \end{equation}$

上述误差式的取值也可以表示为：$\prod_mZ_m$。绘图的代码如下：

import numpy as np
import matplotlib.pyplot as plt
import time
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import zero_one_loss
from sklearn import datasets
import matplotlib.pyplot as plt

# Construct dataset
# 创建8000数据 4个特征 2个类
X, Y = datasets.make_hastie_10_2(n_samples=12000, random_state=1)


n_split = 2000

X_train, X_test = X[n_split:], X[:n_split]
Y_train, Y_test = Y[n_split:], Y[:n_split]

train_errors = []
test_errors = []

num = 350

# Create and fit an AdaBoosted decision tree
bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3),
                        algorithm="SAMME",
                        n_estimators=num)

bdt.fit(X_train, Y_train)

for train_error, test_error in zip(bdt.staged_predict(X_train), bdt.staged_predict(X_test)):
    train_errors.append(zero_one_loss(train_error, Y_train))
    test_errors.append(zero_one_loss(test_error, Y_test))

x = np.linspace(1, num, num)
plt.style.use('ggplot')
plt.plot(x, train_errors, 'r', label='SAMME Train Error')
plt.plot(x, test_errors, 'b', label='SAMME Test Error')
plt.legend(loc='upper right', fancybox=True)
plt.xlabel('Eestimator Numbers')
plt.ylabel('Error Rate')
# plt.show()
plt.savefig('error_rate.png', dpi=250)

结语

提升方法还有更多的应用空间，如提升树，回归树。梯度提升等。即可以在一个分类器中建立更多的层数，而不只是分为简单的$x>v_1$时和$x<v_1$时，用更多的层数来提高分类的准确性。

甚至可以和神经网络相结合，给不同的网络赋予不同的权重，最终决策。

为什么不在这里写？因为我忘了决策树里的一些东西，也忘记了回归树如何实现，等下次再写吧。

还有一点，本文提到的算法已经过时，本文的是SAMME版本的算法，目前已经发布SAMME.R版本的算法且准确率更高，也等下次再写吧。

参考

站在巨人的肩膀上，我们能走得更好：

Just for Life.

提升方法（上）——基于AdaBoost：SAMME