核函数

有一些数据，想“看看”它长什么样，基于高中的知识，我们一般会画频率分布直方图（Histogram）。但基于大学的知识，此时也可以用核密度估计，因为之前的知识水平让我们默认为频率等于概率，但实际情况不一定如此。

这里的“核”是一个函数，用来提供权重。例如高斯函数 (Gaussian) 就是一个常用的核函数。举个例子，假设我们现在想买房，钱不够要找亲戚朋友借，我们用一个数组来表示 5 个亲戚的财产状况： [8, 2, 5, 6, 4]。我们是中间这个数 5。“核”是一个权重函数，假设这个核函数的取值为[0.1, 0.4, 1, 0.3, 0.2]，以此来代表同的亲戚朋友亲疏有别。

在借钱的时候，关系好的朋友出力多，关系不好的朋友出力少，于是我们可以用权重来表示。总共能借到的钱是： $8\times 0.1 + 2\times 0.4 + 5\times 1 + 6\times 0.3 + 4\times 0.2 = 9.2$。

那么“核”的作用就是用来决定权重，例如高斯函数（即正态分布），呈现出距离中心越远，权重越小；反之，距离中心越近，权重越大的特点。核函数还有以下重要的性质：

$\int_{-\infty}^{+\infty}K(x)\text{d}x=1$
$K(-x)=K(x)$

核密度估计

如果我们画频率分布直方图，其实目的是画出“概率密度函数”，因为统计直方图的组距无限接近于0时，得到的函数就是概率密度函数。

但直方图本质上是认为频率等于概率，但这种假设不是必然的。

核密度估计方法是一种非参数估计方法，非参数估计法指：如果一个估计问题所涉及的分布未知或不能用有穷参数来刻划，称这种估计为非参数估计。非参数估计是一种“平滑(smooth)”的手段：设 $(x_1,x_2,\cdots,x_n)$ 是独立同分布的 $n$ 个样本点，于是我们的估计：

$\hat{p}(x)=\frac{1}{n}\sum_{i=1}^nK_h(x-x_i)=\frac{1}{nh}\sum_{i=1}^nK(\frac{x-x_i}{h})$

上面式子中 $x−x_i$ 要提前归一化到 $[-1, 1]$ 之间。

这个公式的意思相当于是“我说的你可能不信，一起看看别人怎么说我的你就信了”。别人是指除自己外的其他样本点，距离越远的样本点权重越小，说话没有分量；距离样本点越近则权重越大，说话的可信度也就越高。当然权重的大小取决于实际采用的核函数，也可能距离越远权重越大，这里只是举个例子。

其中距离的远近通过$x-x_i$的大小来衡量。相当于加权平均后，就能更好地了解我了，于是乎得到新的函数值作为这一点概率的取值。$h$ 是人为指定的，代表“朋友圈”的大小，正式的叫法是“带宽”(bandwidth)，且带宽越大曲线越平滑。

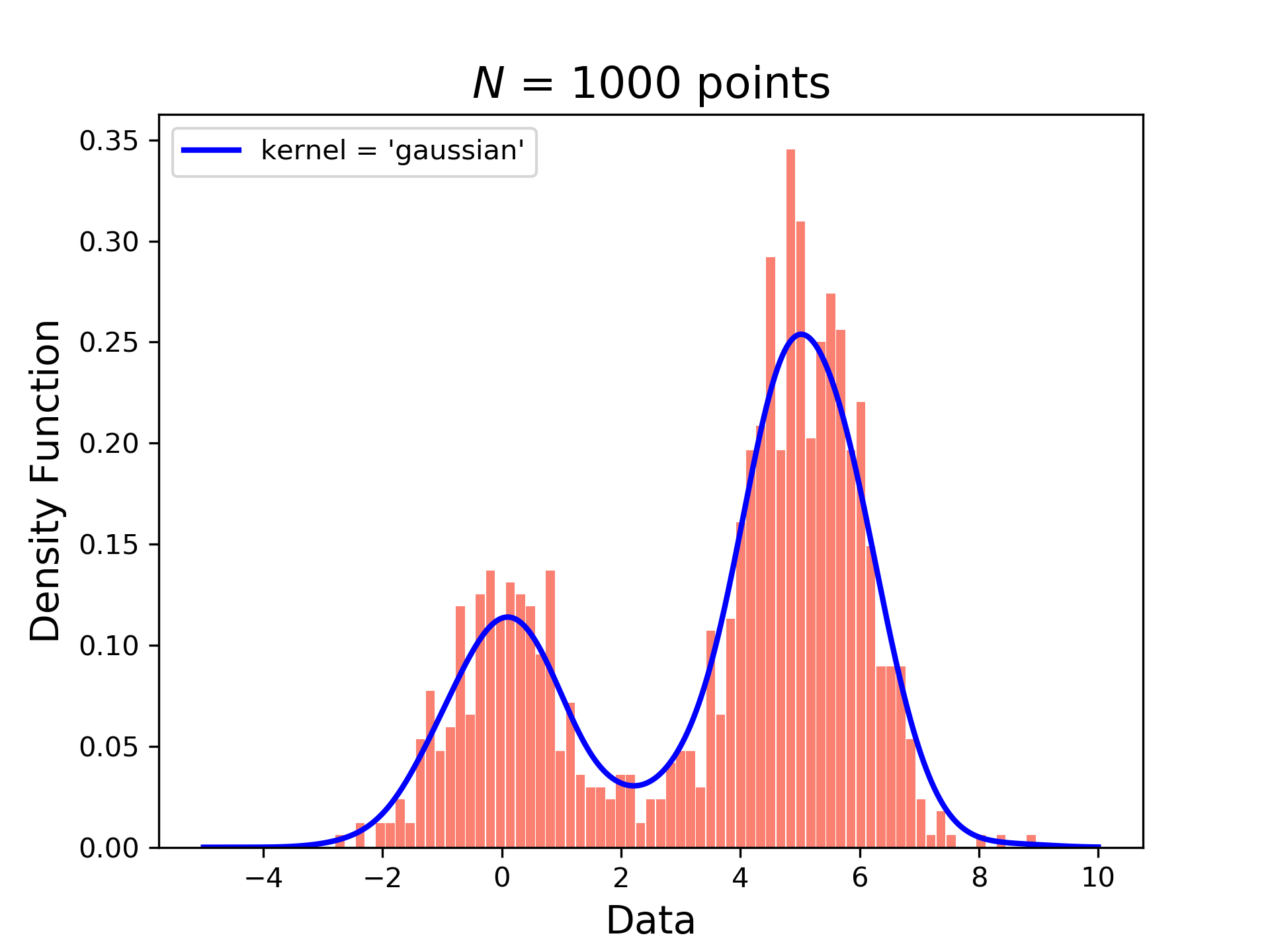
看一下核密度估计和频率分布直方图就能更好的理解了，蓝色的线为概率密度估计，橙色的柱状图为数据出现的频率统计。

核密度聚类

当然文章到这里还没有结束，要是到这里结束我就真成了抄袭文章的了。这组数据看上去很有聚类的趋势不是么，有两种聚类方法：

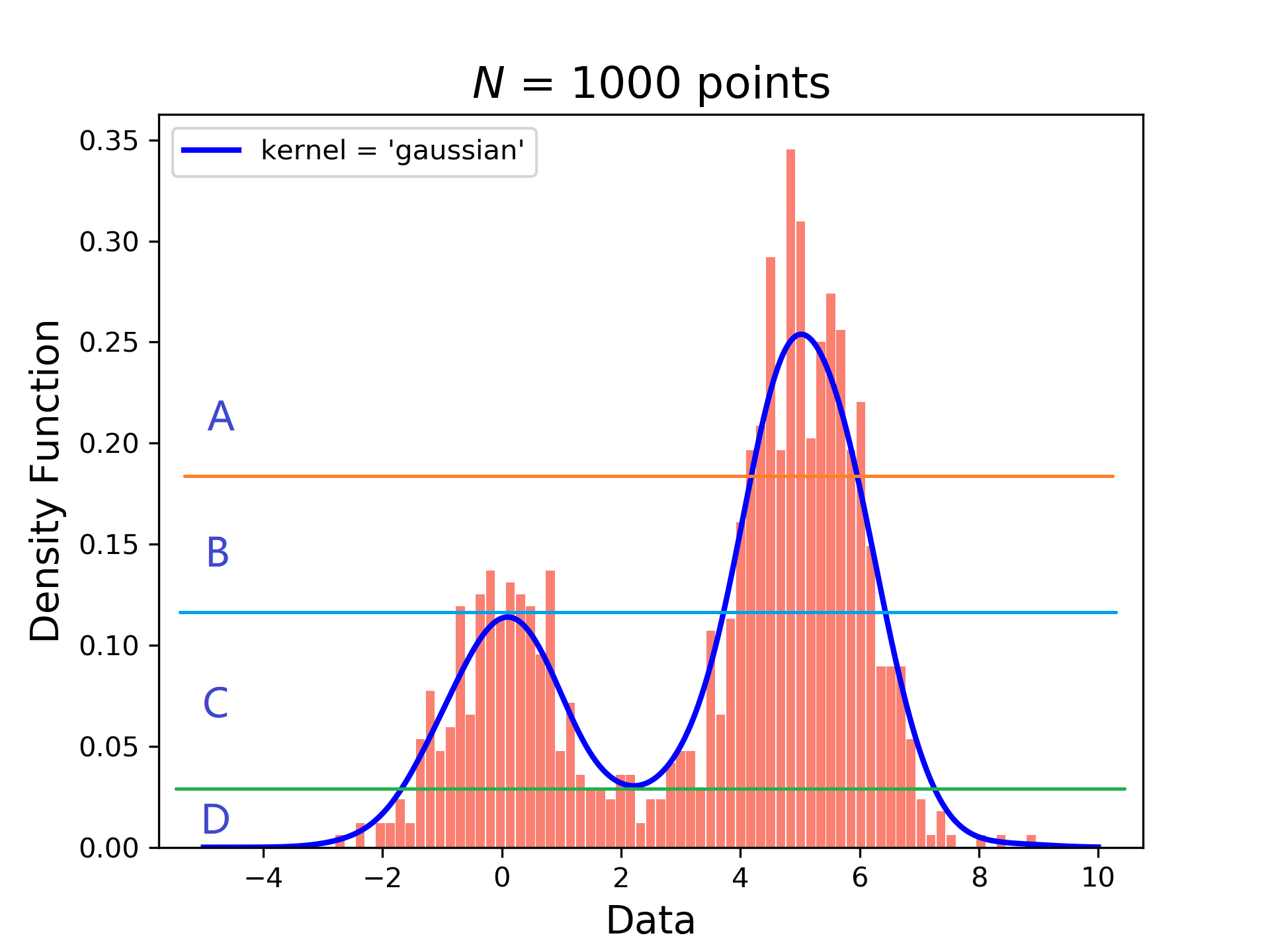
第一种方法。取曲线中的极大值和极小值分成几个区间，将数据的出现频率完成分类，此时会将出现频率相近的数据聚合在一起。按出现频率的高低分为四个居间A,B,C,D共四个类。则A类的数据出现频率最高，D类的数据出现频率最低。如下图所示：
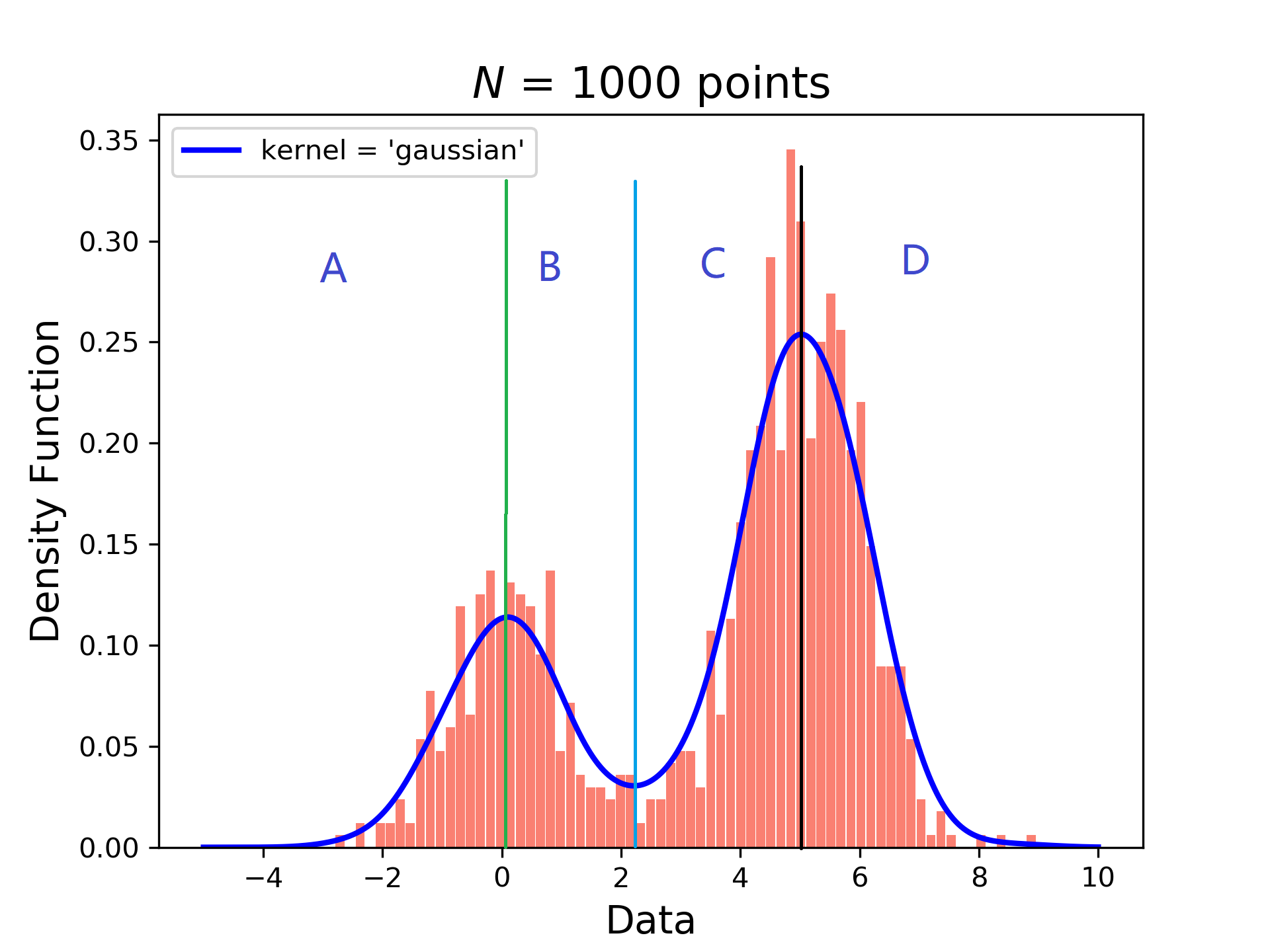
第二种方法。既然曲线有多个极大值和极小值，那么何不以极大值极小值为分界点进行划分区间？按极值点的横坐标取值将数据分为四个居间A,B,C,D共四个类。那么此时对数据的含义也有了要求，即：每个数据段都有不同的含义，不能以数据出现的频率进行笼统划分。如下图所示：举个例子：图片的灰度值的取值范围是[0,255]，假设[0,50]区间数据的出现频率和[200,255]区间数据的出现频率相近，但一定不能把这两组数据放在一起，因为前者代表黑色图层，后者代表白色图层。此时应以极大值、极小值等极值点的横坐标的取值划分区间，而后进行聚类更为合适。
无论哪种方法，都能自动确定聚类数量。

核密度估计

本文着重实现第二种聚类方法，第一种其实同理。

首先产生一组随机数：

N = 1000
np.random.seed(1)
# concatenate 用来组合两种数据，第一组数据均值0方差1，数量占 30% 
# 第二组数据均值 5 方差1 数量占 70%
# [:, np.newaxis] 把数据维度更新为二维一列的数据
X = np.concatenate((np.random.normal(0, 1, int(0.3 * N)), np.random.normal(5, 1, int(0.7 * N))))[:, np.newaxis]

其次调用sklearn这个库实现核密度估计即可：

X_plot = np.linspace(-5, 10, 1000)[:, np.newaxis]

colors = ['blue']
kernels = ['gaussian']
lw = 2

for color, kernel in zip(colors, kernels):
    # Fit the Kernel Density model on the data.
    kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X)
    # Evaluate the log density model on the data. 
    log_dens = kde.score_samples(X_plot)
    plt.plot(X_plot[:, 0], np.exp(log_dens), color=color, lw=lw,
            linestyle='-', label="kernel = '{0}'".format(kernel))
    arr = np.exp(log_dens)
    np.save('data.npy', arr)

X_plot ：An array of points to query；
kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X) 完成训练工作，计算核密度；
log_dens = kde.score_samples(X_plot) 评估这点的概率值该是多少。画图是连续的曲线，曲线上的点不一定在样本中，所以要弥补一些缺失的点；
np.exp 是因为kde.score_samples反馈结果的概率值取了ln(可参看源码实现)，所以计算真实概率值要exp一下；
保存数据用于后期聚类处理。

完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from scipy.stats import norm

N = 1000
np.random.seed(1)
X = np.concatenate((np.random.normal(0, 1, int(0.3 * N)), np.random.normal(5, 1, int(0.7 * N))))[:, np.newaxis]

X_plot = np.linspace(-5, 10, 1000)[:, np.newaxis]

colors = ['blue']
kernels = ['gaussian']
lw = 2

for color, kernel in zip(colors, kernels):
    kde = KernelDensity(kernel=kernel, bandwidth=0.5).fit(X)
    log_dens = kde.score_samples(X_plot)
    plt.plot(X_plot[:, 0], np.exp(log_dens), color=color, lw=lw,
            linestyle='-', label="kernel = '{0}'".format(kernel))
    arr = np.exp(log_dens)
    np.save('data.npy', arr)

plt.legend(loc='upper left')
plt.hist(X, 70, normed = 1, histtype='bar', facecolor='salmon', rwidth=0.9)  
# plt.set_xlim(-4, 9)
# plt.set_ylim(-0.02, 0.4)

plt.title("$N$ = 1000 points", fontsize=16)
plt.xlabel("Data", fontsize=14)
plt.ylabel("Density Function", fontsize=14)
plt.savefig('test.png', dpi=300)

求极值以聚类

之后借助scipy求出核密度估计的点中的几个极大值和极小值（极值并不唯一）

import numpy as np
from scipy.signal import argrelextrema
# 加载数据
data = np.load('data.npy')
# 求极大值
maxn = argrelextrema(data, np.greater)
# 求极小值
minn = argrelextrema(data, np.less)
# 打印极大值的索引
print(maxn)
# 打印极小值的索引
print(minn)

输出结果如下：

1 2	(array([340, 667], dtype=int64),) (array([480], dtype=int64),)

得到的结果显示有两个极大值两个极小值，与概率密度估计图象相吻合。按照返回的极值索引访问极值即可。

1	print(data[minn])

进而按照极值划分数据，即可完成聚类。

参考

站在巨人的肩膀上，我们能更好的前行：

你也可以看到我查看翻阅了大量的官方文档，其实对于这种技术东西，官方文档的解释往往是最好的，不懂的问题就多动动手多思考嘛，哪能不懂就问。