博客的进阶使用：在指定位置插入脚注¹，这样就不用在文末列出参考文献，显得对不上号了。回归正题，如果不出什么特别大的意外，就应该去搞网络安全了。注：此网络安全非彼网络安全，指：对抗样本而非网络入侵。所以准备来开个坑，先整理基础知识，基础不劳，地动山摇。

问题背景

所谓对抗样本，即向原始样本中添加一些人眼无法察觉的噪声，这样的噪声不会影响人类的识别，但是却很容易欺骗 DNN ²，使其作出与正确答案完全不同的判定。如下图所示，使用基于梯度³的攻击方式，很容易欺骗神经网络：

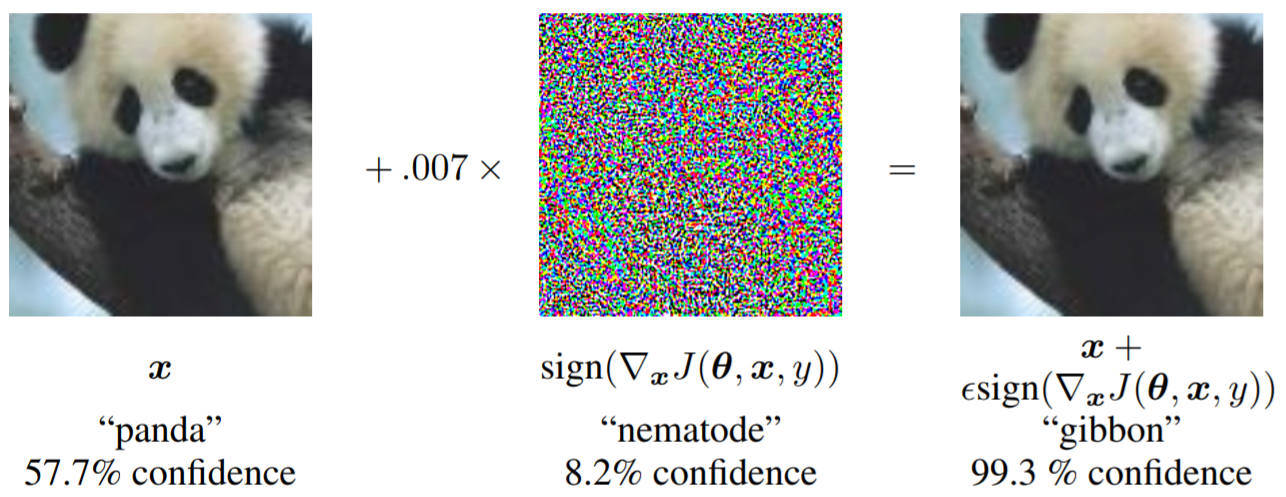
将肉眼不可见的细小扰动加入到原图中，网络识别出粗，甚至有 99.3% 的概率认为这是长臂猿。试想，如果犯罪分子将人烟稀少地区的交通信号牌改为立即停车，人眼不会觉得有什么不妥，但是无人驾驶系统却会乖乖停车，那么此时车上人员的安全何以保障？将禁止右转改为右转，造成交通事故就只在弹指一挥间了。究其本质原因，还是因为现有的 DNN 不能完全区分哪些特征是对分类有用的，哪些是可以忽略的。

基本概念

白盒攻击：攻击者能够获知机器学习所使用的算法，以及算法所使用的参数。
黑盒攻击：攻击者并不知道机器学习所使用的算法和参数，但攻击者仍能与机器学习的系统有所交互，比如可以通过传入任意输入观察输出，判断输出。
无目标攻击：对于一张图片，生成一个对抗样本，使得标注系统在其上的标注与原标注无关，即只要攻击成功就好，对抗样本的最终属于哪一类不做限制。
有目标攻击：对于一张图片，生成一个对抗样本，使得标注系统在其上的标注与目标标注完全一致，即不仅要求攻击成功，还要求生成的对抗样本属于特定的类。

基于梯度的攻击算法

FGSM 攻击算法

设 $x$ 是原始样本，$x’$ 是对抗样本，其中：$x’ = x + \eta$，为了让对抗样本不被机器所识别，$\eta$ 应该足够小，这里使用无穷阶范数来表述 $\eta$ 足够小这一限制：$\Vert \eta \Vert_\inf < \epsilon$。事实上，常说的 $l_\inf-\text{ball}$ 就是这个意思。

考虑输入层对对抗样本的线性变换：

\begin{equation}
w^Tx’=w^Tx+w^T\eta
\end{equation}

如果假设 $\eta = \text{sign} (w)$，$w$ 是一个 $n$ 维的矩阵，每一维的模长是 $m$，那么经过线性映射后，输入将增大 $\epsilon mn$。尽管 $\Vert \eta \Vert_\inf$ 不会变换，但随着维度的升高、矩阵权重的变换和非线性激活，回导致最终结果变化很大。这也就是为什么对抗样本与原始样本相差无几，但却产生了不同的输出。

因此，FGSM³ 产生对抗样本的方式为：

\begin{equation}
\eta=\epsilon \text{sign} \big( \nabla_x J(\theta, x, y) \big)
\end{equation}

其中，$J$是分类损失函数，通过梯度上升，最大化损失函数，企图使得原始的 $x$ 不在属于 $y$ 类。~~好坏啊~~。torch 官方⁵也给出了对抗样本的程序：

# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
    # Collect the element-wise sign of the data gradient
    sign_data_grad = data_grad.sign()
    # Create the perturbed image by adjusting each pixel of the input image
    perturbed_image = image + epsilon*sign_data_grad
    # Adding clipping to maintain [0,1] range
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # Return the perturbed image
    return perturbed_image
def test():
    data_grad = data.grad.data

    # Call FGSM Attack
    perturbed_data = fgsm_attack(data, epsilon, data_grad)

    # Re-classify the perturbed image
    output = model(perturbed_data)

PGD 攻击算法

PGD 攻击算法⁶是 FSGM 的变体，它即是产生对抗样本的攻击算法，也是对抗训练的防御算法。

论文先抛出了两个问题：

如何产生强有效的对抗样本，只需要一点点扰动就可以欺骗神经网络？
如何训练模型，使得没有对抗样本轻易能欺骗网络？

在论文中，为了防止网络只能抵御某一特定类型的攻击，应该保证模型有足够的对抗鲁棒性，接下来，使用一种方法来训练模型，达到这种保证。在传统的网络中，损失函数通常是优化网络参数 $\theta$，使得损失函数达到最小：$\mathbb{E}_{x\sim D}[L(x,y,\theta)]$。但是，对于对抗样本而言，就是要误导神经网络的输出。同样，这篇论文中，对抗样本的扰动范围也限制在 $l_\inf-\text{ball}$ 内。

但是在训练损失函数$\mathbb{E}_{x\sim D}[L]$之前，先考虑对抗样本的扰动，所以先不把干净样本 $x$ 输入到网络，而是用对抗样本作为网络的输入。所以论文的公式将攻击和防御放入统一框架内，对抗训练就是在一个马鞍面内求鞍点。

\begin{equation}
\min \mathbb{E}_{x\sim D} \big[ \max_{\sigma\in S} L(\theta, x, y) \big]
\end{equation}

其中的 $S$ 表示球面限制，即无穷范数不能超过 $S$。这个统一的框架包括了内部最大化和外部最小化，因此可以视为鞍点问题，也清晰的描述了鲁棒模型应该达到的目标。内部最大化的期望是，寻找最优的对抗样本达到很高的损失；外部最小化的期望是，寻找模型参数，能抵抗对抗样本的攻击。所以，最终训练得到的模型也具有稳定的对抗鲁棒性。

在攻击部分，对抗样本的制作方法为：

\begin{equation}
x+\epsilon \text{sign} \big( \nabla_x L(\theta, x, y) \big)
\end{equation}

这可以解释为内部期望最大化的单步攻击。但多步攻击会更加有效，因为 DNN 是复杂的非线性映射，不要企图一步到位。在数据点的 $l_\inf$ 球边界的许多点运行PGD，来探索损失函数中的大部分位置，即在这个球的范围内，探索到绝大多数地方，以能够找到最强的对抗样本。虽然在 $x_i+S$ 的范围内有许多局部最大值，但是他们的损失值往往相似，也就是说，解决了最大化内部非凹函数的问题。

\begin{equation}
x^{t+1}=\prod_{x+S}\bigg(x^t+\epsilon \text{sign} \big( \nabla_x L(\theta, x, y) \big)\bigg)
\end{equation}

$\prod_{x+S}$ 符号的意思是，先计算原图像的损失梯度得到对抗样本，对抗样本减去原图像得到扰动值，并通过 torch.clamp 限制在球面范围内，原图像加上扰动值就是最终的对抗样本。还是看代码吧：

def pgd_attack(model, images, labels, eps=0.3, alpha=2/255, iters=40) :
    images = images.to(device)
    labels = labels.to(device)
    loss = nn.CrossEntropyLoss()
    # 原图像
    ori_images = images.data

    for i in range(iters) :
        images.requires_grad = True
        outputs = model(images)

        model.zero_grad()
        cost = loss(outputs, labels).to(device)
        cost.backward()
        # 图像 + 梯度得到对抗样本
        adv_images = images + alpha*images.grad.sign()
        # 限制扰动范围
        eta = torch.clamp(adv_images - ori_images, min=-eps, max=eps)
        # 进行下一轮对抗样本的生成。破坏之前的计算图
        images = torch.clamp(ori_images + eta, min=0, max=1).detach_()

    return images

实验发现，通过PGD发现的局部最大值在正常训练的网络和对抗训练的网络中都有着相似的损失值；换句话说，PGD 训练对抗样本，和普通网络训练干净样本的损失是类似的；这也说明，只要能够防御住PGD，就会对所有的一阶攻击手段具有鲁棒性。

补充

剩下的这些都是论文中实验部分所提及的了，更多内容，还可以参考这里⁷的解读和这里⁸的代码。

在模型容量较小时，模型对 FGSM 对抗样本产生了过拟合，这种行为被称为label leaking。而且，模型无法防御 PGD 攻击。
对抗样本的复杂性，是决策边界也变得复杂，因此模型需要更大的容量，才能抵御对抗样本。

常见防御算法

对抗训练：对抗训练旨在训练一个更加鲁棒的模型，其训练集由真实数据集和加入了对抗扰动的数据集组成，因此叫做对抗训练。
去噪模块：在输入模型进行判定之前，先对当前对抗样本进行去噪，剔除其中造成扰动的信息，使其不能对模型造成攻击。

上述几种防御类型对对抗样本扰动都具有一定的防御能力，效果参差不齐。本来想都放到这篇博客里，后来发现任务量太大了，后续我会读一些论文，列举一些代表性算法。当然，也可以移步这里，有很多关于网络安全算法⁴的介绍。

程序

使用 ResNet50 制作对抗样本，攻击类型为黑盒攻击，使用 VGG16 作为目标模型，程序 ⁹ 放到了 Github。

攻击算法	目标模型	原始准确率	扰动0.05	扰动0.1	扰动0.15	扰动0.3
FGSM	VGG16	94.27	52.52	47.37	42.86	32.24
PGD	VGG16	94.27	43.01	31.53	23.92	14.53

Just for Life.

对抗攻击篇：FGSM 与 PGD 攻击算法