在对抗攻击中,有人尝试着去用对抗样本攻击目标检测的网络。但是,检测网络与分类网络不同,检测网络还有检测器,存在 RPN、ROI-Align 以及边界框回归器等。而分类接受的图像来自检测器的输出,并不是原始的输入。所以只在图片上产生细微的扰动很可能不起做作用 1。所以衍生出了一些基于 patch (补丁)的攻击。
Adversial Patch
这篇论文 2 是最开始的,创建一些通用的小 patch,可以放到任何场景下去干扰分类,使得网络忽略真实的物体,而输出诱导的错误分类。传统的对抗攻击,都是在输入上叠加一些微小的扰动,人眼察觉不出来的那种,但需要修改图像中的每一个像素,对于 $1000\times 1000$ 的像素点,需要操作一百万个像素点,在现实世界难以应用。
而本文中,不在满足这一约束,而是生成一个独立于任何场景(光照、角度)的 patch 放到图片的任何位置,相反,这个 patch 大于只有 $20\times 20$ 的大小,所以这个计算量是可以在现实世界应用的。这个 patch 很容易被网络看到,但仍然可以导致网络错误的输出。当 patch 使用了很大的扰动,传统的防御算法只能防御小扰动的样本,对大扰动的样本鲁棒性反而很差,毕竟数据分布不同。如下所示:

所以,这个补丁攻击的仍然是分类网络。
训练方式
在全部数据集上进行训练,对 patch 进行各种各样的转换、缩放、旋转,这个 patch 允许被设置为任何形状。对于给定图像 $x$,patch $p$,位置 $l$,变换 $t$,定义一个补丁操作 $A(p,x,l,t)$,将 $t$ 应用到 $p$ 上,在把 $p$ 放到 $x$ 的 $l$ 位置。
而 patch 是经过训练的,以诱导网络输出错误的标签 $\hat{y}$,这个训练过程为:
\begin{equation}
p = \arg \max_p \mathbb{E}_{x\sim X,t\sim T, l\sim L}[\log P(\hat{y}|A(p,x,l,t))]
\end{equation}
$X$ 是训练数据的分布,$T$ 是 patch 变换的分布,$L$ 是位置。通过这个公式,生成的 patch 会忽略背景,所以生成的 patch 通用性较强。而为了伪装 patch,使得最终的 patch 不太离谱,加入了一个限制 $|p-p_{orig}|_\inf < \epsilon$。
DPATCH
这个补丁 3 就正儿八经的攻击目标检测的网络了。不同于上一个补丁只误导分类器,同时也攻击边界框回归器,以产生错误的定位。其实目标检测是很难攻击的,毕竟有很多 anchor 和候选框,样本不一定能被选中。攻击目标检测的网络时,与传统分类不同的是,需要定位到不同大小的目标及其位置。
在无目标攻击中,让检测器不能检测到物体的位置,所以最大化真实类别和边界框回归器的损失,这里的类别 $y$ 是背景类。也就是,通过放置补丁,让网络的将真实的目标视为背景。
\begin{equation}
P_u=\arg \max_P \mathbb{E} [L(A(x,s,P);y;B)]
\end{equation}
在有目标攻击中,目标是只能检测到 patch 而忽略其它真正的目标。所以需要最小化 patch 的类别损失和边界损失,类别是自己选择的误导类别。也就是,让网络将补丁视为目标。
\begin{equation}
P_t=\arg \min_P \mathbb{E} [L(A(x,s,P);y_t;B_t)]
\end{equation}
$A(x,s,P)$ 表示将补丁 $P$ 通过变换 $s$ 添加到图像 $x$ 上。在补丁进入网络前,首先先添加一个随机噪音,而后定义 patch 的边界框。训练流程如下:
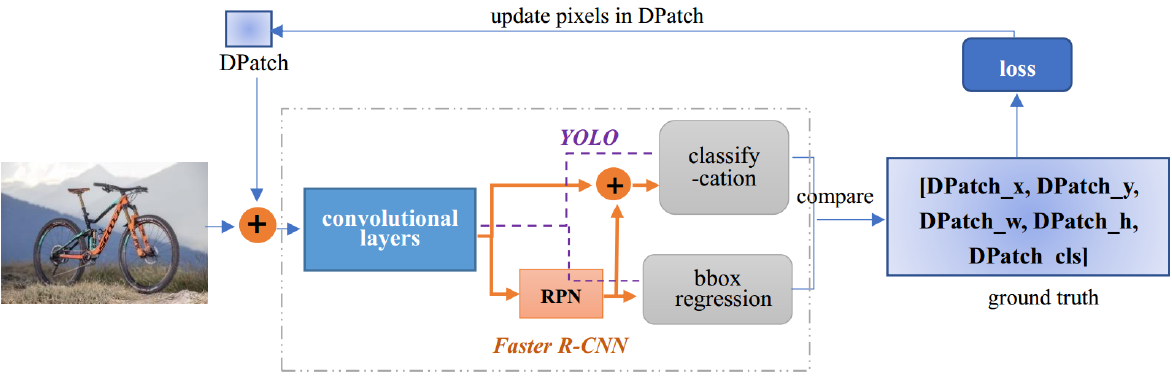
- 为了分析不同位置下 DPATCH 的影响,随机对 DPATCH 的位置进行变换,而保持像素点数值不变,在每轮训练时候都随机初始化变换 $s$
- 为了分析不同类别下 DPATCH 的影响,将 DAPTCH 的类别都设置为人,随机指定了四个类别
- 为了分析不同大小的 DPATCH 的影响,所以做了一些实验,分别分析 20 40 80 大小的 DPATCH 对结果的影响
实验结果大概证明了,DAPTCH 在可以出现在图片的任何位置,更大的 DAPTCH 攻击性更强。
DPATCH 起作用的原因:DPATCH 的攻击目标就是目标检测网络,使得 ROI 提取到的区域被 DPATCH 覆盖,所以提取到的 ROI 区域,将会忽略其它目标。如果攻击成功了,许多提取到的 ROI 应该会有 DPATCH 的存在。为此,统计每个区域被提取为 ROI 的次数,也发现那里正好是 DPATCH 出现的地方。故此验证了攻击成功的原因是:DPATCH 欺骗了检测器,使得 ROI 含有 DPATCH,而不是正常目标,如下图所示:
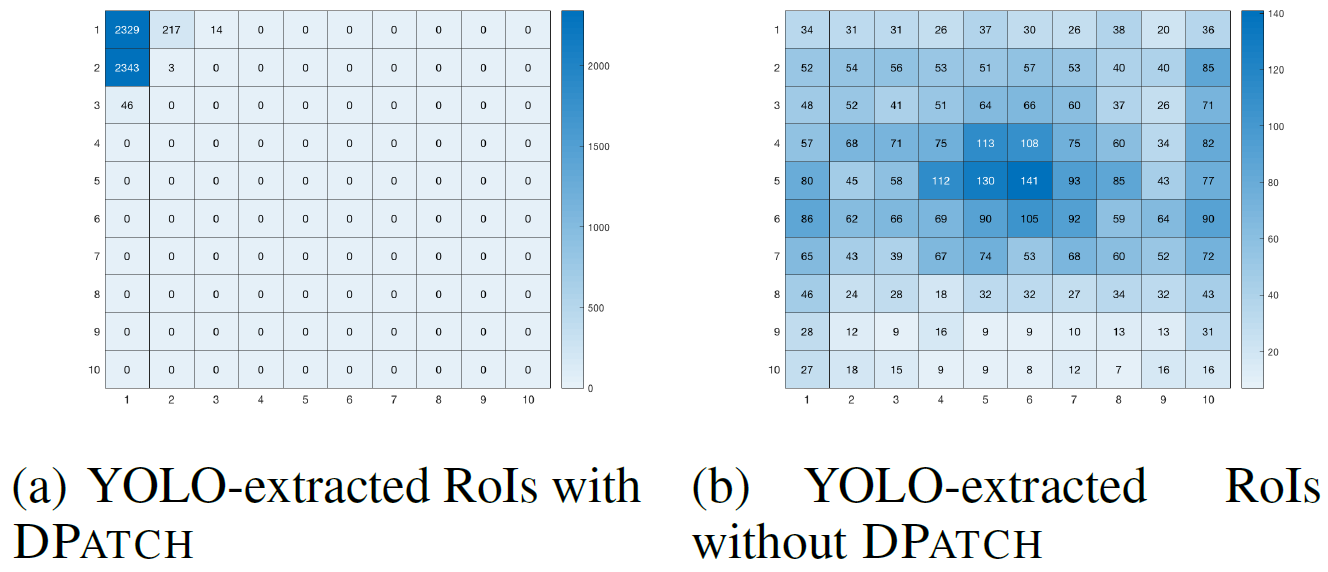
物理世界的补丁
这篇论文 4 做了一个演示视频。与之前不同的是,不需要 patch 放到图像上误导分类和检测,而是设计了一个 patch 抑制其它目标的表达。所以可以 patch 到任何地点甚至是远离目标的地点。而且不需要训练位置参数,且不需要修改场景中的目标。
本文构造一个物理上的 patch,放到图像中,抑制其它目标的表达。寻找与制作 patch 的方式也很简单:
\begin{equation}
\arg \max_{\delta} \mathbb{E}_{(x, y) \sim D, t\sim T} [L(h_\theta(A(\delta, x, t)), y)]
\end{equation}
其中 $\delta$ 是补丁,$D$ 是数据分布,$T$ 是变换分布,$A$ 是将补丁 $\delta$ 经过 $t$ 变换放到 $x$ 上。但是,对 $\delta$ 的最大期望可能会超出预期,所以不够通用。所以像 PGD 一样,让扰动朝着其它目标移动:
\begin{equation}
\delta := \delta - \alpha \nabla_\delta [L(h_\theta(A(\delta, x, t)), \hat{y})]
\end{equation}
但是事实证明这种做法很差。所以尝试最大化与真实目标的损失,不对补丁设置任何的边界框和目标类别,而是直接抑制检测的其它类别:
\begin{equation}
\delta := clip_{[0,1]} (\delta + \alpha \nabla_\delta [L(h_\theta(A(\delta, x, t)), y)])
\end{equation}
这种方法成功的原因和上述的 DPATCH 是一样的,提取到的 ROI 还有 PATCH。作者和 DPATCH 做了对比,分析 DPatch 之所以时好时差,是因为它将 patch 放到了 ground truth box 的周围,patch 最终驻留在一个单一的单元中。这意味着损失由『负责』该单元的 rpn 控制。只要补丁被识别,模型在预测所有其他对象时受到的惩罚就很小,且边界框或类标签上不会受到惩罚。所以在实践中,补丁经常被检测到,但是,并没有抑制其他目标被检测。反而言之,一旦 patch 没被检测到,网络还是能识别到目标。
而在本文的方法中,patch 可以置于任何位置,当 patch 与任何一个 ground truth box 重叠都会造成损失,也就是,当前目标检测失败。当模型不能预测任何 ground truth box 时,损失增加最多。
references
- 1.为什么难以攻击目标检测网络 ↩
- 2.Adversial Patch ↩
- 3.DPATCH ↩
- 4.物理世界的补丁 ↩

