MART(Misclassification Aware adveRsarial Training) 是 2020 年提出的最好的对抗防御算法。传统对抗训练算法中 min-max 时不会考虑当前样本是否被正确分类,统一制作对抗样本。而作者抓住了这一点,发现对于 max 制作对抗样本期间没有被网络正确分类的样本,对结果的影响很大。换句话说,网络连干净样本都不认识,何谈认识它的对抗样本? MART 算法的创新点在于区别对待错分类和正确分类的样本。
背景
MART 防御的仍然是微小扰动的图像,也就是人眼察觉不出来的那种。论文用$p$ 范数满足这一限制:$\Vert x’-x \Vert_p \leq \epsilon$。对抗训练可以视为使用对抗样本进行数据增强,解决的是以下优化问题:
\begin{equation}
\min_\theta \frac{1}{n} \sum_{i=1}^{n} \max_{\Vert x’-x \Vert_p \leq \epsilon} L(h_\theta(x_i’), y_i)
\end{equation}
$n$ 是一个 batch 的大小,$L$ 是分类的损失函数。内部通过最大化损生成对抗样本,外部最小化对抗样本的分类损失来训练更好的 DNN,如 PGD 就是使用的这种方案。
而本文的关注点在对抗训练的对抗样本上,其实许多对抗训练算法忽略了一点,有些样本被正确分类,有些样本被错误分类,但无论哪种样本,都在 min-max 中直接制作对抗样本。因此本文也就抛出例如下疑问:
由错分类样本和正确分类的样本产生的对抗样本,对模型的鲁棒性贡献程度是一样的吗?如果不是,如何利用这个差异,来提升模型的鲁棒性?
本文针对这个被忽略的一点做了一些探索,发现被错分类和正确分类的样本对最终模型的鲁棒性的确有不同的影响。
本文做了这样的实验,在 CIFAR-10 数据集上做白盒攻击,扰动值 $\epsilon=8/255$。使用 PGD-10 算法制作对抗样本,以对抗训练的形式训练得到的网络的准确率是 87%。然后选择被错分类的样本记为 $S^-$,在选择被正确分类的样本记为 $S^+$。之后使用这两类样本,用不同的方式训练上述网络,最后用 PGD-20 算法制作的对抗样本评估最终模型的鲁棒性。结果如下图所示:
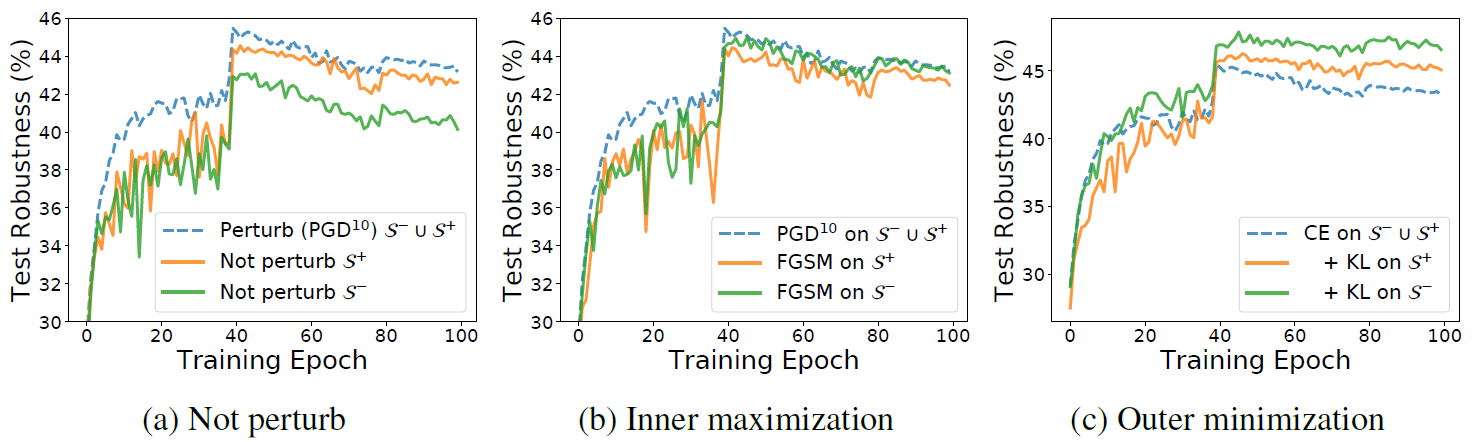
在图 a 中:错分类样本对鲁棒性有明显影响。
- 蓝色的线是标准对抗训练的对抗鲁棒性
- 绿色的线表示没有对 $S^-$ 制作对抗样本,其它样本仍然是对抗样本,鲁棒性降低很大;
- 橙色的线表示没有对 $S^+$ 制作对抗样本,其它样本仍然是对抗样本,鲁棒性变换其实不大。
图 b 中:为了更深理解『错分类样本和其它样本』的影响是不同的,外部 min 采用交叉熵,内部 max 采用攻击强度很弱的 FGSM 算法:
- 蓝色的线是标准对抗训练的对抗鲁棒性
- 绿色的线表示在 $S^-$ 上产生的对抗样本对鲁棒性几乎没有提升。这可以说明不同的 max 方法在 $S^-$ 上会对模型鲁棒性有不同程度的影响。然而,
- 橙色的线表示,低强度的攻击算法在 $S^+$ 上制作的对抗样本会使鲁棒性退化。
图 c 中,内部 max 选择 PGD-10 算法,外部 min 尝试不同的函数。发现对错分类的样本使用不同的 min 方法,对最终鲁棒性的结果影响也很大。
- 蓝色的线是,对传统对抗训练,外部 min 使用交叉熵函数
- 绿色的线是,对错分类样本添加额外的 KL 散度作为正则化项,鲁棒性有明显的提升
- 绿色的线是,将同样的 KL 散度作为正则化项添加到正确分类的样本上,鲁棒性也有提升,但不如绿色的线明显。
基于以上实验发现,论文考虑了错分类样本对鲁棒性的影响,提出了一个新的防御算法,以一种动态的方式实现对抗训练。主要贡献是:
- 研究了错分类和正确分类的样本对『对抗训练』最终鲁棒性的影响,结果表明,在 min-max 框架下,对错分类样本的处理对模型最终鲁棒性的影响佷大,且 min 方法比 max 方法更为关键。
- 提出一种正则化的对抗风险,将错误分类的样本做显式区分,作为正则化项添加到损失函数中。
MART 算法
临时通知一周后期末考试,去准备期末考试了,考完了回来填坑。其实这个算法的缺陷显而易见,可以尝试往 GAN 那边走一走。考完了,回来填坑。
前期定义
对于一个 $K$ 分类问题,给定数据集 $(x_i,y_i)$,深度模型 $h_\theta$,对于每个样本而言,网络的输出如下:
\begin{equation}
\begin{aligned}
h_\theta(x_i) &= \arg \max p_k(x_i, \theta) \\
p_k(x_i, \theta) &= \exp(z_k(x_i,\theta)) / \sum_{j=1}^K \exp(z_j(x_i,\theta))
\end{aligned}
\end{equation}
其中,$z_k(x_i,\theta)$ 是网络的逻辑输出,softmax 后获得类别标签。对抗风险定义为:一个 batch 中被分类错误的样本数除以 batch 数。对抗样本的制作为:
\begin{equation}
\hat{x} = \arg\max \mathbb{I}(h_\theta(x_i) \neq y_i)
\end{equation}
算法
注,原文第二章写了一些0-1损失,后面又说不用这个,所以我没有写0-1损失
首先将训练样本分为正样本 $S^+_{h\theta}$ 和错样本 $S^-_{h\theta}$,即能被网络正确识别的样本和不能被正确识别的样本。
- 对于 $S^-_{h\theta}$ 而言,添加正则化项,使得网络能稳定的防御错分类对抗样本。因为对抗样本的分类需要更强的分类器和更光滑的决策边界,损失函数定义为 $\mathbb{I}(h_\theta(\hat{x_i}) \neq y_i) + \mathbb{I}(h_\theta(x_i) \neq h_\theta(\hat{x_i}))$,意思是,第一项优化的目标是,使对抗样本被分类正确;第二项优化的目标是,使网络认识原始样本和对抗样本。
- 对于 $S^+_{h\theta}$ 而言,正则化不会明显提升网络鲁棒性。在这种情况下,已经有 $h_\theta(x_i)=y_i$,因此此时的优化目标是 $\mathbb{I}(h_\theta(x_i) \neq h_\theta(\hat{x}))=\mathbb{I}(h_\theta(\hat{x_i})\neq y_i)$,也就是说,网络将干净样本和对抗样本视为两个类别且对抗样本分类错误的概率。
- 其中 $\mathbb{I}$ 是指示函数,意思是,错了损失值为1,正确损失值为0。
但是这个指示函数难以优化,本文提出 BCE(boosted cross entropy) 损失函数,用于代替 $\mathbb{I}(h(\hat{x} \neq y))$,定义如下:
\begin{equation}
\begin{aligned}
\text{BCE}(p(\hat{x}, \theta), y_i) &= -\log(p_{y_i}(\hat{x},\theta)) - \log (1-\max_{k\neq y_i}p_k(\hat{x}, \theta))
\end{aligned}
\end{equation}
第一项是普通的交叉熵损失函数,第二项用于提升模型决策边界的间隙。
使用 $KL$ 散度代替 $\mathbb{I}(h_\theta(x) \neq h_\theta(\hat{x}))$,定义如下:
\begin{equation}
\text{KL}(p(x_i,\theta)||p(\hat{x}, \theta))=\sum_{k=1}^K p_k{(x_i,\theta)} \log \frac{p_k(x_i,\theta)}{p_k(\hat{x_i},\theta)}
\end{equation}
对于制作对抗样本使用的指示函数 $\mathbb{I}(h_\theta(x_i) \neq y_i)$,通过 $1-p_{y_i}(x_i, \theta)$ 的形式选择对抗样本。因此,内部最大化的损失定义如下,攻击方式选择 PGD。
\begin{equation}
\hat{x} = \arg \max \text{CE} (p(x_i, \theta), y_i)
\end{equation}
将两中损失结合起来到对抗训练的框架中,最终的损失函数为:
\begin{equation}
L = \text{BCE}(p(\hat{x}, \theta), y_i) + \lambda \text{KL} (p(x_i,\theta)||p(\hat{x}, \theta))(1-p_{y_i}(x_i, \theta))
\end{equation}
$\lambda$ 参数用于平衡两个损失。

