在之前 yolox 解析与改进 的文章中,提到了使用 CIoU Loss 改进 SimOTA 分配正样本机制导致的小目标检测精度低的问题,就顺手来整理一些常用定位损失与演化过程。本文所有的图,绿色为 Truth,蓝色为预测结果。
IoU Loss
这个是最常见的定位 loss,假设预测框为 $A$,目标框为 $B$,那么 IoU Loss 就是:
\begin{equation}
L = 1 - \frac{A\cap B}{A \cup B}
\end{equation}
同样这个 loss 会带来一些问题:
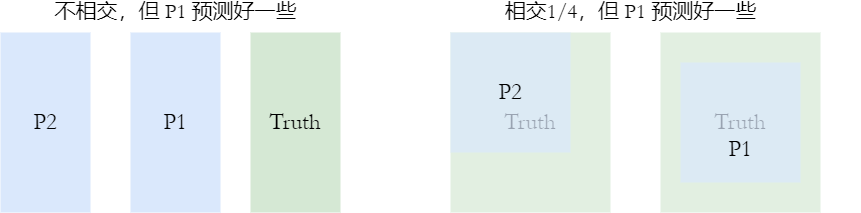
- 当 $A$ 和 $B$ 没有交集的时候,损失恒定为 1
- 当 $A\cap B$ 为定值时,直观上某些相交情况并不好
GIoU Loss
为了缓解 $A$ 和 $B$ 没有交集的时候,损失恒定为 1 的缺陷,GIoU Loss 的表示如下:
\begin{equation}
L = 1 - IoU + \frac{A_c - U}{A_c}
\end{equation}
$A_c$ 是包含预测结果和真实标注数据的最小覆盖矩形。当最小覆盖矩形越小,损失也就越小。但是实际使用中这个损失的表现可能不是很好,因为目标检测都会有样本匹配机制,根据 IoU 匹配筛选出来的正样本至少能和真实标注相交。
DIoU Loss
为了解决上述的 $A\cap B$ 为定值时,直观上某些相交情况并不好的缺陷,或者说,期望使预测结果落在真实数据的中心位置:
\begin{equation}
L = 1 - IoU + \frac{\rho^2 (b, b^{gt})}{c^2}
\end{equation}
其中 $\rho$ 是预测结果中心点和真实框中心点的距离,$c$ 是最小闭包区域对角线的长度。
CIoU Loss
在目标检测中,目标常常有着不同的尺寸,如下图所示,在 IoU 取值固定的情况下,右侧的预测结果更符合目标框的尺寸。
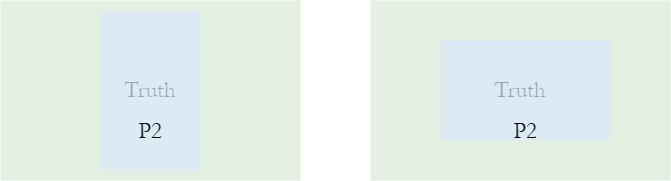
因此做了如下的修改:
\begin{equation}
\begin{aligned}
L &= 1 - IoU + \frac{\rho^2 (b, b^{gt})}{c^2} + \alpha v \\
\alpha &= \frac{v}{(1-IoU) + v} \\
v &= \frac{4}{\pi^2} \bigl( arc \tan \frac{w^{gt}}{h^{gt}} - arc \tan \frac{w}{h} \bigr) \\
\end{aligned}
\end{equation}
如果 IoU 越大,那么 $\alpha$ 也会越大,公式的最后一项也会越大。由于 $arc \tan$ 的取值范围是 -1 到 1,且当 $x$ 较为接近时,$y$ 也接近,那么就期望两者的长宽比越来越接近。
$\alpha-IoU$ Loss
$\alpha-IoU$ Loss 是在之前的一些列 IoU Loss 上进行的修改,增加了 $\alpha$ 这个指数,实验显示 $\alpha=3$ 比较有效。
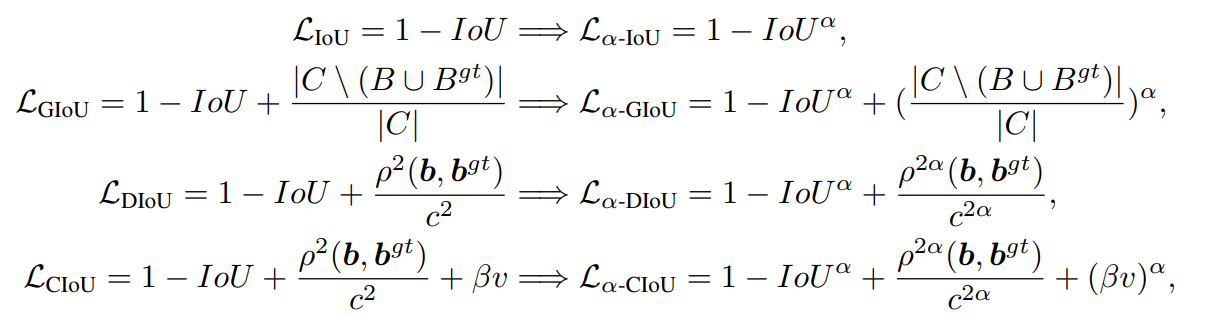
以简单的 IoU Loss 来可视化一下这是为什么。我们可视化一下 IoU Loss 和 $\alpha-IoU$ Loss ,得到如下的图:
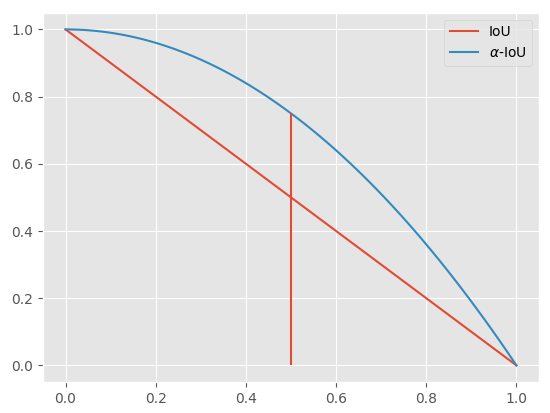
在 $x=0.5$ 之后,$\alpha-IoU$ 显示收敛的梯度更大。因为目标检测会根据 IoU 为预测结果分配真实框,因此不用太担心 IoU 很小的情况,当然这一部分可以手动修改。
L1, L2, Smooth-L1 Loss
这个 loss 的形式比较简洁:
\begin{equation}
L = |x-y|
\end{equation}
也就是预测坐标和目标坐标相减的绝对值。而 L2 loss 的形式则是预测值和目标值差的平方:
\begin{equation}
L = (x-y)^2
\end{equation}
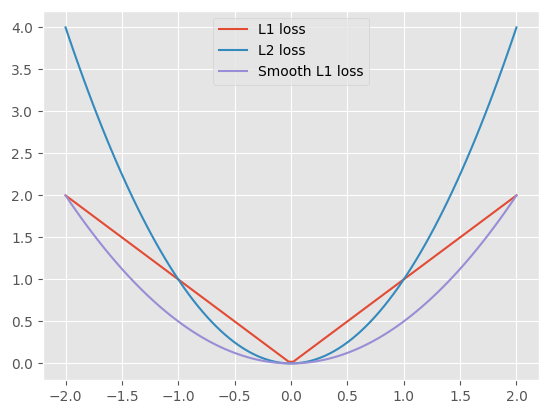
如下图所示:
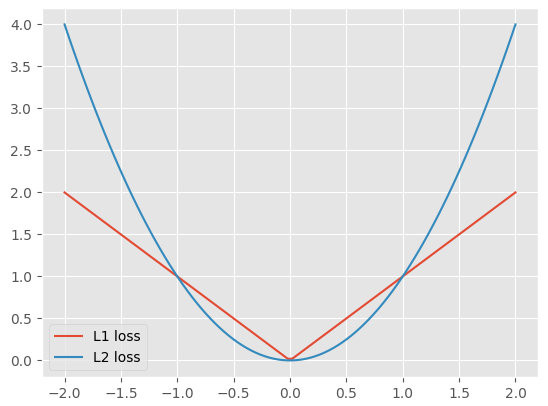
- 对于 L1 loss,在 -1 左侧和 1 的右侧收敛稳定,但是 -1 到 1 之间表示目标很接近了,应该减缓梯度
- 对于 L2 loss,在 -1 左侧和 1 的右侧呈现爆炸增长,存在梯度爆炸、异常值敏感的缺陷,但是 -1 到 1 之间梯度较为缓和
而 Smooth Loss 综合了两者的优点,得到新的表达形式:
\begin{equation}
L(x) =
\begin{cases}
0.5x^2 &, |x| \leq 1 \\
|x|-0.5 &, \text{otherwise} \\
\end{cases}
\end{equation}