Just for Life.

明月更几时

0%

算法系列：树

发表于 更新于
本文字数： 12k 阅读时长 ≈ 10 分钟

树是数据结构中很重要的一种结构，在现实生活中常用于表达层次关系和非单一的映射关系，如一个老板下对应有多个员工。通过一段时间的算法练习，本文将树常见的算法收录整理，包括：

  • 求二叉树叶子节点的数量
  • 求节点权重和
  • 求距离根节点最近、最远的叶节点
  • 求每一层节点的数量
  • 遍历二叉树，求给定权值的路径
  • 二叉查找树

而对于红黑树、2-3-4树等较为复杂的树结构，本文暂时不收录，仅收录较为简单容易理解的，本文适用于：编程不太好、但了解基本数据结构的人，你仅仅需要知道深度优先遍历、广度优先遍历、二叉树的根节点、普通节点、叶子节点的区别即可。

一类通常题目：求树的叶子数量，求每一层的节点数量，求树的最大高度，求叶子权重的和，都可以归类为对二叉树的遍历，所以本文更多的是树的遍历算法(深度优先或广度优先)的应用。其次，先序、中序、后序遍历树，对遍历顺序有严格的要求，一般不用此类方法遍历树去求解上述问题，一般都是解决先序中序转后序此类需求，在后续会写出此类问题的求解算法。

警告：尽管文本做了详细的代码注释和讲解，但如果你只是准备靠本文的讲解企图理解代码，恐怕不太行，还需要自己多加练习和多思考。

树

构建

654. 最大二叉树

给定一个不重复的整数数组 nums。 最大二叉树可以用下面的算法从 nums 递归地构建:

  • 创建一个根节点，其值为 nums 中的最大值。
  • 递归地在最大值 左边 的 子数组前缀上 构建左子树。
  • 递归地在最大值 右边 的 子数组后缀上 构建右子树。
  • 返回 nums 构建的 最大二叉树 。

示例 1：

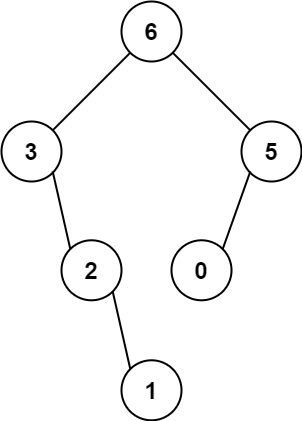
1
2
3
4
5
6
7
8
9
10
11
12
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

树的算法主要依赖于递归，假设有这么一个递归函数，返回的是所需要的节点，牢牢记住这一点。如果实在理解不了递归，那么只需要理解在调用这个函数的时候，知道它返回的是所需的节点即可。

递归函数就是自己调用自己，因此需要确定好参数的类型和数量，因此下次还会用到这个函数。我们看一下这个题，根据数组创建树，如果找到了最大值，最大值左侧就是左子树，右侧就是右子树。而左右子树就需要索引来区分，不能越界，也就是说，不能把其他的节点放到当前子树中。因此，我们假定递归需要三个参数，数组 nums，子树的起点索引 l 和终点索引 r。

  1. 第一次调用递归函数，传入的参数是 nums, 0, nums.size()。然后找到数组中的最大值，创建节点。假设最大值的索引是 idx
  2. 递归调用函数，创建节点的左子树，那么创建左子树的递归就是 nums, 0, idx
  3. 递归调用函数，创建节点的右子树，那么创建左子树的递归就是 nums, idx+1, nums.size()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return build(nums, 0, nums.size());
    }
    // build 就是返回需要的节点
    TreeNode* build(vector<int>& nums, int l, int r) {
        // 树的越界一定在函数最开始检查
        if (l >= r) {
            return nullptr;
        }
        int maxv = -1;
        int idx;
        // 找最大值和对应的索引
        for (int i = l; i < r; i++) {
            if (nums[i] > maxv) {
                maxv = nums[i];
                idx = i;
            }
        }
        // 当前节点
        TreeNode* node = new TreeNode(maxv);
        // 当前节点的左子树
        node->left = build(nums, l, idx);
        // 当前节点的右子树
        node->right = build(nums, idx + 1, r);
        // 返回创建的，最大值根节点
        return node;
    }
};

遍历

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为：对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

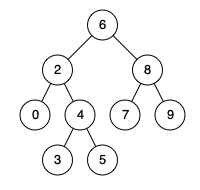
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

这个算后续遍历了，因为要找两个节点的公共祖先，起码要先知道子节点在哪里，知道了子节点才能找到父节点。

  • 后序遍历时，如果遇到了要找的子节点，那么计数
  • 当计数满足条件时，当前节点就是深度最大的公共祖先
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    TreeNode* res = nullptr;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        postorder(root, p, q);
        return res;
    }

    int postorder(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr)
            return 0;
        int a = 0;
        // 子树返回的值
        int r1 = postorder(root->left, p, q);
        int r2 = postorder(root->right, p, q);
        a += (r1 + r2);
        // 当前节点是否满足，因为一个节点可以是自己的祖先
        if (root == p) {
            a += 1;
        }
        if (root == q) {
            a += 2;
        }
        // 如果满足条件，那么找到的节点就是深度最大的公共祖先
        if (a == 3 && res == nullptr) {
            res = root;
        }
        // 返回当前子树的状态
        // 1 表示找到了 p
        // 0 表示没找到 q 和 p
        // 2 表示找到了 q
        // 3 表示都找到了
        return a;
    }
};

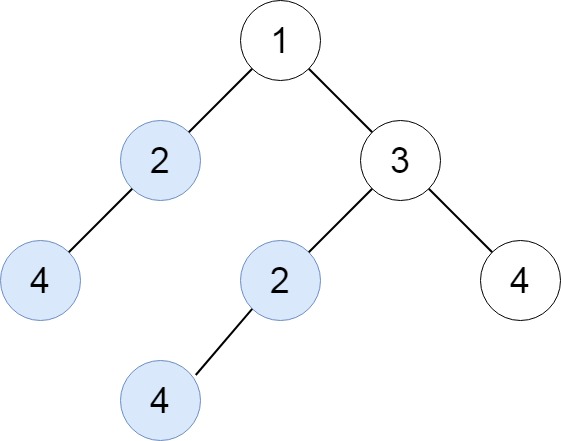
652. 寻找重复的子树

给定一棵二叉树 root，返回所有重复的子树。对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

  • 我们可以用深度优先遍历，去遍历一个节点及其子树，将数值拼接起来得到一个字符串。如果存在相同的字符串，就说明存在相同的子树
  • 根据题意，我们知道需要检查每一个节点对应的子树的结果
  • 也就是说，检查每一个节点需要遍历，而生成节点对应的结果又需要一次遍历，总共需要两次遍历。第一次遍历是为了遍历节点，第二次遍历是为了得到字符串。这两次遍历的任务不同，我们要写两个遍历函数
  • 那么在第一次遍历二叉树的时候，加入第二次遍历去得到字符串即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    vector<TreeNode*> res;
    unordered_map<string, int> m;
    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        build(root);
        return res;
    }

    // 第一次遍历
    void build(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        string s = "";
        // 得到当前节点的结果，第二次遍历
        dfs(root, s);
        m[s] += 1;
        if (m[s] == 2) {
            res.push_back(root);
        }
        build(root->left);
        build(root->right);
    }

    void dfs(TreeNode* root, string& s) {
        if (root == nullptr) {
            s += "+";
            return;
        }
        s += "=";
        s += to_string(root->val);
        dfs(root->left, s);
        dfs(root->right, s);
    }
};

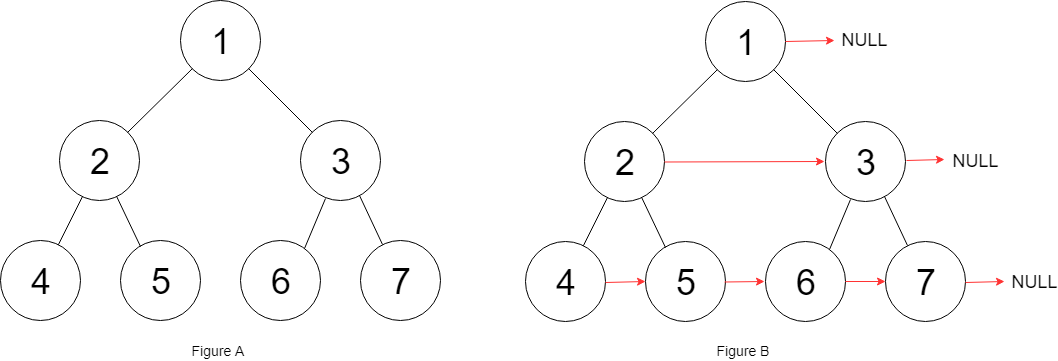
递归

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。初始状态下，所有 next 指针都被设置为 NULL。

根据前文我们知道，递归是自己调用自己，且需要明确参数的数量和内容，这样才能方便的调用。如果理解不了递归的细节，就知道要让递归实现什么，直接调用即可，不要陷入递归的细节。

在这个题中，我们发现需要造作两个指针 a 和 b，这两个指针是根节点的孩子，而且需要让 a 指向 b，子树也是如此。也就是说，递归有两个参数。因此，只需要传入两个参数，递归的处理左右子树即可，在递归函数中，完成 a 指向 b 的功能即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) {
            return nullptr;
        }
        // 由于是完美二叉树，因此根节点必然有两个孩子
        build(root->left, root->right);
        return root;
    }

    void build(Node* left, Node* right) {
        if (left == nullptr || right == nullptr) {
            return;
        }
        // 修改指针方向
        left->next = right;
        // 处理左子树
        build(left->left, left->right);
        // 处理右子树
        build(right->left, right->right);
        // 左子树的右节点，需要指向右子树的左节点，参考图片的最后一行叶子节点中间部分
        build(left->right, right->left);
    }
};

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同。

同样，我们只需要定义递归函数，并实现其功能即可。根据题意，这个递归函数的作用就是展平子树，实现这个函数后，递归的实现左右子树的展平，不必陷入递归的细节。而且，是先要展平子树，在展平当前节点，因为只有保证子树是展平的，才能保障当前节点可以展平。

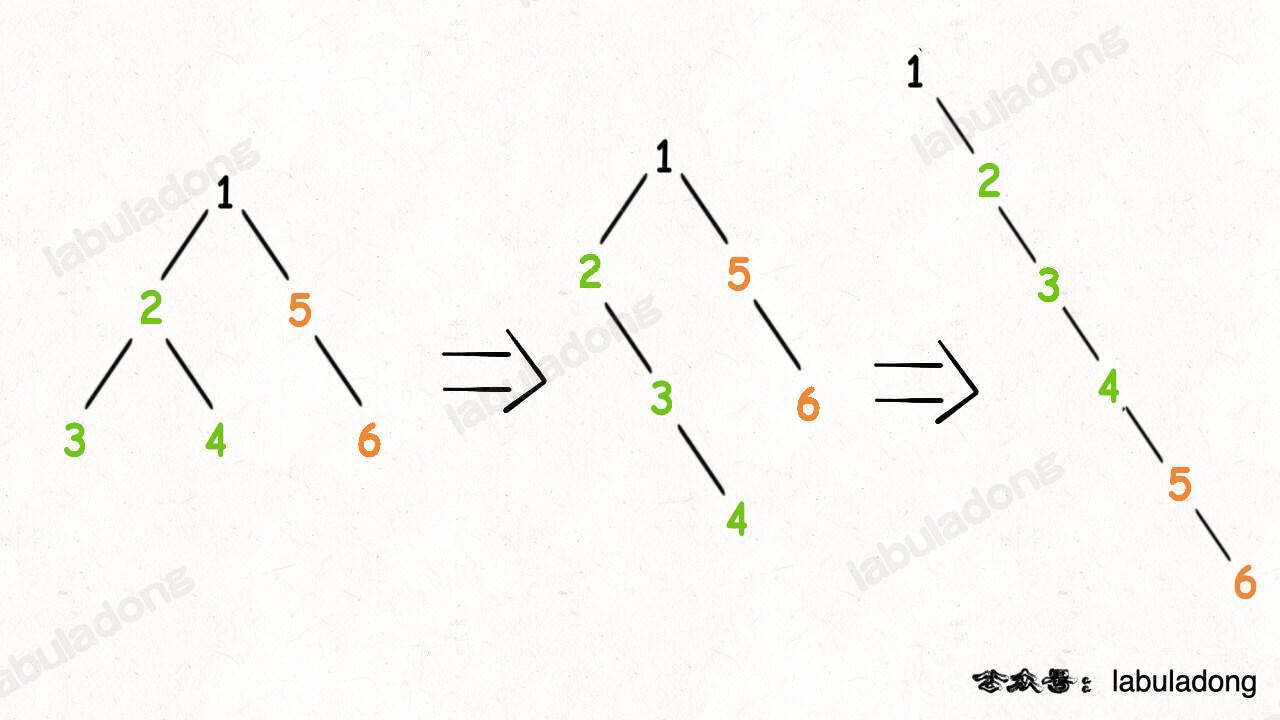
  • 如上图所示，先展平左右子树，直接 flatten(left) 和 flatten(right) 即可
  • 在展平之后，根节点的右指针指向左子树，然后移动到左子树的末尾，在指向右子树即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    void flatten(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        // 展平子树
        flatten(root->left);
        flatten(root->right);
        // 根节点对应的左右子树
        TreeNode* l = root->left;
        TreeNode* r = root->right;
        // 右指针指向左子树
        root->right = l;
        // 左子树为空
        root->left = nullptr;
        // 移动到左子树的末尾
        TreeNode* p = root;
        while (p->right != nullptr) {
            p = p->right;
        }
        // 左子树指向右子树
        p->right = r;
    }
};

前缀树

208. 实现 Trie (前缀树)

Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true；否则，返回 false 。

我想不到什么好的语言来描述前缀树。简单说一下就是，假设用树来查单词，单词字母都是小写。那么树的每个节点都有 26 个孩子，初始化为空。

比如对于 cat 这个单词，根节点有 26 个孩子，c 节点不为空，c 节点有 26 个孩子，a 不为空，a 节点有 26 个孩子，t 不为空，且 t 节点设置一个结束符，表示 cat 这个单词到 t 这里就结束了。

因此我们能在这个树中查到 cat 这个单词。浪费空间？不是的，转念一想，为 cat 这个单词建的树，是不是能容纳所有的长度为 3 的单词？and,but,how 等单词都能存进来，且能实现 $O(1)$ 时间的查找。

说了这么多，看一下这个树如何实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Trie {
public:
    vector<Trie*> child;
    bool end;
    // 26 个孩子和结束符
    Trie() {
        child.resize(26);
        end = false;
    }

    void insert(string word) {
        Trie* node = this;
        for (auto ch : word) {
            int a = ch - 'a';
            // 所有的孩子节点中，这个字母对应的节点不为空
            if (node->child[a] == nullptr) {
                node->child[a] = new Trie();
            }
            // 构建孩子节点的子节点
            node = node->child[a];
        }
        // 结束符，表示这个单词到此结束
        node->end = true;
    }
    // 搜索同理
    bool search(string word) {
        Trie* node = this;
        for (auto ch : word) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                return false;
            }
            node = node->child[a];
        }
        // 如果搜索的不是结束符，返回 false
        // 如 apple 在词表中，但 app 不在
        // 不能返回 true
        if (node->end == false)
            return false;
        return true;
    }
    
    bool startsWith(string prefix) {
        Trie* node = this;
        for (auto ch : prefix) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                return false;
            }
            node = node->child[a];
        }
        return true;
    }
};

211. 添加与搜索单词 - 数据结构设计

请你设计一个数据结构，支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。

实现词典类 WordDictionary ：

  • WordDictionary() 初始化词典对象
  • void addWord(word) 将 word 添加到数据结构中，之后可以对它进行匹配
  • bool search(word) 如果数据结构中存在字符串与 word 匹配，则返回 true ；否则，返回 false 。word 中可能包含一些 ‘.’ ，每个 . 都可以表示任何一个字母。

由于 . 可以代表任何一个字符，因此需要对 . 进行处理，使其可以表示任何一个字母。不过这就需要递归处理来使得程序优美一些：

1
2
3
4
5
6
7
8
9
// 代表 26 个字母
for (int i = 0; i < 26; i++) {
    // 只要不为空，就依次检查
    if (node->child[i] != nullptr) {
        if (subsearch(word, idx + 1, node->child[i]) == true) {
            return true;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class WordDictionary {
public:
    vector<WordDictionary*> child;
    bool end = false;
    WordDictionary() {
        child.resize(26);
    }

    void addWord(string word) {
        WordDictionary* node = this;
        for (auto ch : word) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                node->child[a] = new WordDictionary();
            }
            node = node->child[a];
        }
        node->end = true;
    }

    bool subsearch(string word, int idx, WordDictionary* node) {
        if (idx >= word.size()) {
            return node->end;
        }
        auto ch = word[idx];
        if (ch == '.') {
            for (int i = 0; i < 26; i++) {
                if (node->child[i] != nullptr) {
                    if (subsearch(word, idx + 1, node->child[i]) == true) {
                        return true;
                    }
                }
            }
        } else {
            int a = ch - 'a';
            if (node->child[a] != nullptr) {
                if (subsearch(word, idx + 1, node->child[a]) == true) {
                    return true;
                }
            }
        }
        return false;
    }

    bool search(string word) {
        return subsearch(word, 0, this);
    }
};

/**
 * Your WordDictionary object will be instantiated and called as such:
 * WordDictionary* obj = new WordDictionary();
 * obj->addWord(word);
 * bool param_2 = obj->search(word);
 */

648. 单词替换

在英语中，我们有一个叫做 词根(root) 的概念，可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如，词根 an，跟随着单词 other(其他)，可以形成新的单词 another (另一个)。

现在，给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根，则用最短的词根替换它。你需要输出替换之后的句子。

就是前缀树的基础应用了，因为需要寻找最短的前缀，因此遇到结束符就立刻返回；如果查找不到这个单词，那么就返回空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Tree {
public:
    vector<Tree*> child;
    bool end = false;
    Tree() {
        child.resize(26);
    }
    void insert (string& word) {
        Tree* node = this;
        for (auto ch : word) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                node->child[a] = new Tree();
            }
            node = node->child[a];
        }
        node->end = true;
    }
    string search(string& word) {
        Tree* node = this;
        string res = "";
        for (auto ch : word) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                return "";
            } else {
                res += ch;
                node = node->child[a];
                if (node->end == true) {
                    return res;
                }
            }
        }
        return "";
    }
};

class Solution {
public:
    string replaceWords(vector<string>& dictionary, string sentence) {
        Tree node;
        for (auto it : dictionary) {
            node.insert(it);
        }
        string res, tmp;
        stringstream ss{sentence};
        while (ss >> tmp) {
            res += " ";
            auto a = node.search(tmp);
            if (a != "") {
                res += a; 
            } else {
                res += tmp;
            }
        }
        return res.substr(1);
    }
};

677. 键值映射

设计一个 map ，满足以下几点:

  • 字符串表示键，整数表示值
  • 返回具有前缀等于给定字符串的键的值的总和

  • 实现一个 MapSum 类：

  • MapSum() 初始化 MapSum 对象

  • void insert(String key, int val) 插入 key-val 键值对，字符串表示键 key ，整数表示值 val 。如果键 key 已经存在，那么原来的键值对 key-value 将被替代成新的键值对。
  • int sum(string prefix) 返回所有以该前缀 prefix 开头的键 key 的值的总和。

这个题也比较简单，假设 apple 对应的值为 5，而后插入 app 值为 3，那么 ap 前缀对应的和就是 8，也就是在 5 的基础上加了 3。如果再次插入 apple 此时值为 4，那么 ap 前缀对应的和就是 7，且 apple 对应的值是 4。

如此我们可以看到，只有插入存在过的单词时，才会修改数值。由于插入不存在的单词，数值的更新方式是 +=，参考上述例子。为了统一这一点，我们需要设置一个 map，并记录本次插入的值。

如果这个字符串是第二次插入，那么就需要对值进行修改，比如 apple 第一次是 5，map 存入 5；第二次是 3，那么 += 的值就应该是 -2，map 存入 3。如果第三次是 6，那么加等于的值就是 3，map 存入 6。也就是，+= 的数值就是本次插入的值减去 map 中存入的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class MapSum {
public:
    vector<MapSum*> child;
    int cnt = 0;
    unordered_map<string, int> m;
    MapSum() {
        child.resize(26);
    }
    
    void insert(string key, int val) {
        MapSum* node = this;
        int v = val;
        if (m.count(key)) {
            v = val - m[key];
        }
        m[key] = val;
        for (auto ch : key) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                node->child[a] = new MapSum();
            }
            node = node->child[a];
            node->cnt += v;
        }
    }
    
    int sum(string prefix) {
        MapSum* node = this;
        for (auto ch : prefix) {
            int a = ch - 'a';
            if (node->child[a] == nullptr) {
                return 0;
            }
            node = node->child[a];
        }
        return node->cnt;
    }
};

/**
 * Your MapSum object will be instantiated and called as such:
 * MapSum* obj = new MapSum();
 * obj->insert(key,val);
 * int param_2 = obj->sum(prefix);
 */

参考

本文构最初思于 2019 年 6 月通过刷题学习数据结构时期，第一次整理发表于 2020 年 2 月。本文全部参考了柳神的程序，而非我本人的原创。但是我都花精力研究了程序、重写程序、最后做了归纳整理。

时间流转，2022 年由于找工作的需要，又开始整理一些 leetcode 题目，PAT 题目过于简单也从本文中删去退出了历史舞台，但我依然敬佩柳神，也从她的程序中受益颇多。

如果你初学数据结构或刷题，我强烈建议做一下 PAT 的基础题目掌握数据结构，也建议观摩柳神的程序。

本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章