鲁迅有云：能用的程序不等于好的程序（他没说过）。在近期处理图数据时，经常性的要遍历边和点，这就很容易造成高时间复杂度的算法。且，当数据在一万左右时，复杂度$O(n^2)$的算法根本跑不动，在中等规模的服务器上也会卡死。

在不断的写程序中，降时间复杂度降出了经验，遂整理如下。我也发现了，我不喜欢写XX快速入门之类的文章，比如翻译pytorch的文档写一下pytorch快速入门的文章，的确很吸引流量，但我不喜欢，更喜欢整理自己的经验。

问题背景

以处理图数据为例，尤其是需要不断遍历边和点的场景；
没有真实的代码，全部是伪代码；（直接放工程代码会很大，从工程里摘出对应代码来仍然是伪代码）
虽然是处理图数据，但依然能适应其他场景。如果你想借鉴思想，不妨看一下，如果不想看，现在退出即可。

借助数据结构

众所周知，图的节点是有度的，这里我们以无向图为例。假设，此时在做图数据的融合，将邻接链表相同的节点视为双胞胎节点融合在一起。此时最明显的哦优化就是借助桶排序，因为邻接链表相同，则节点的度必然相同。按照节点度进行分类，能有效降低复杂度。

假设只融合度数在$[2, 64]$之间的节点。首先，创建基数为 2 到 64 的桶。并按照节点的度，将节点放到对应桶中，即节点度为2就放到基数为2的桶，节点度为16就放到基数为16的桶。这里一切正常：

# 创造节点度的桶
radix = [[] for i in range(2, 67)]
# 按照是否被访问选取节点, 并按照度数放入桶
for ver in graph.vertices():
    # 取节点索引
    ver_idx = graph.vertex_index[ver]
    # 按照是否被访问和节点的度进行筛选
    degree = len(graph.get_all_neighbors(ver_idx))
    if visited[ver_idx] == False and degree >= 2 and degree <= 64:
        # 添加节点的索引
        radix[degree].append(ver_idx)

一般思路，在每个桶内，节点的度是相同的。这时候只需要遍历桶，计算桶内每个节点的邻接链表，若邻接链表相同，则融合。此时便是创建一个字典，以节点的索引为 key，以邻接链表为 value。之后遍历桶生成字典，在遍历字典的 value ，相同则融合。

# 按照桶内的邻接列表进行融合
for bucket in radix:
    # 两个以上的节点才能融合
    if len(bucket) >= 2:
        # 相反，由项找索引，不然时间复杂度太高
        for i in bucket:
            # 按照索引取节点
            # 集合的意思是取消元素顺序的影响，不然顺序会影响判断是否相等 
            # str保证可哈稀
            adj_list[i].append(set(graph.get_out_neighbors(i)))

        # 邻接列表相同的进行融合
        # （这里我实在不知道怎么写了，于是暴力循环了）
        # 复杂度太高，大图测试直接卡死
        for key1 in adj_list.keys():
            for key2 in adj_list.keys():
                if key1 != key2 and adj_list[key1] == adj_list[key2]:
                    if visited[key1] == False and visited[key2] == False:
                        visited[key1] = visited[key2] = True
                        M[key1], M[key2] = key2, key1

如上代码，直接遍历一个桶内部的邻接列表并判断是否相等，复杂度为$O(n^2+n)$。思路很正常，但这种写法实在愚蠢。如果我们换种思路，在字典中，以邻接列表为 key，以节点的索引为 value 呢？那么当两个节点的邻接列表相同时，节点的索引会自动放到字典对应 key 的 value 中，这样就省去了比较的过程。此时时间复杂度为$O(n^2)$。（radix代表基数是 2 到 64 的桶，取值是常数，故计算复杂度时忽略最外层循环）。由此可见，不用额外的数据结构，仅需要简单的变换，就能将时间复杂度从$O(n^2+n)$降低到$O(n^2)$。但实际中这样的点很少，即融合的for循环可以视为$O(1)$，所以算法的执行时间和$O(n)$复杂度的算法相似。

# 按照桶内的邻接列表进行融合
for bucket in radix:
    # 两个以上的节点才能融合
    if len(bucket) >= 2:
        # 相反，由项找索引，不然时间复杂度太高
        adj_reverse = defaultdict(list)
        for i in bucket:
            # 按照索引取节点
            # 集合的意思是取消元素顺序的影响，不然顺序会影响判断是否相等 
            # str保证可哈稀
            adj_reverse[str(set(graph.get_out_neighbors(i)))].append(i)

        # 以邻接列表为键，节点索引为 values
        for values in adj_reverse.values():
            if len(values) >= 2:
                for i in range(0, len(values) - 1, 2):
                    ver1, ver2 = values[i], values[i+1]
                    if visited[ver1] == False and visited[ver2] == False:
                        visited[ver1] = visited[ver2] = True
                        M[ver1], M[ver2] = ver2, ver1

其实这个优化的并不所最好的，另一个是，但涉及的问题背景太深了，直接拿出来怕读者看不懂，就用这个例子凑合了。

好的逻辑

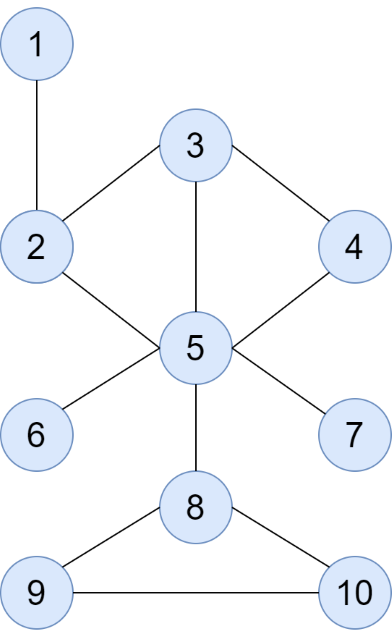
问题描述：此时我们要生成一个图的 k 跳邻接信息，即常见的邻接矩阵是一跳信息。二跳信息就是隔着一个节点还能相邻，那么邻接矩阵中，这两个节点对应的索引取值为 1。可以直接看图，节点 1 和节点 5 就是二跳连接，adj[1][5] = 1，这个意思。假设我们要找三跳信息。

在 networkx 这个包中，判断两个节点是否有路径的方式是使用最短路径，如没有最短路径，这两个节点当然不存在路径，最短路径的复杂度为$O(V+E)$，$V$是节点的数量，$E$是边的数量。伪代码就是has_path(node1, node2)。那么，此时最粗暴的算法来了，遍历节点，若两个节点之间的最短路径等于 3 ，就在邻接矩阵中置为 1。时间复杂度$O(V^2(V+E))$的伪代码：

for node1 in graph.vertices():
    for node2 in graph.vertices():
        if has_path(node1, node2) == 3:
            adj[node1, node2] = adj[node2, node1] = 1

真实数据测试：运行时间 19.098s，图节点数是94，边数是1554。

只要我们稍微打开 API 查询一下，就能知道有 shortes_distance 这种函数，即在时间复杂度$O(V+E)$内求出一个节点到其他所有节点的最短路径，在借助 np.where 或 np.isin 就很容易降低复杂度了，一份$O(V(V+E))$的伪代码：

for node in graph.nodes():
    arr = shortest_distance(node)
    mask = np.where(arr == target)
    for row, col in mask:
        adj[row][col] = adj[col][row] = 1

真实数据测试：运行时间 0.139s，图节点数是94，边数是1554。

那么在冷静分析一下，很多孤立节点并不是我们所需要的，取度数大的节点进行融合，几乎能覆盖图中全部的数据，因为图中大部分点会和度数大的点有联系。那么，我们对图节点按度数排序（堆排的复杂度为 $\log n$），取出前 $\log v$ 个节点，计算他们和图中节点的 $k$ 跳信息。伪代码：

node = sort_by(graph.nodes.degree)[:logv]
for i in node:
    arr = shortest_distance(node)
    mask = np.where(arr == target)
    for row, col in mask:
        adj[row][col] = adj[col][row] = 1

此时算法的时间复杂度是 $O(\log V(V+E))$。一般而言，$E$比$V$大，算法计算时间更取决于 $E$ 的大小。实际数据：运行时间 0.039s，图节点数是94，边数是1554。

Just for Life.

降低算法时间复杂度，以图数据处理为例

问题背景

借助数据结构

好的逻辑