9 月了，虽然开学前还是充满了焦虑和担忧，越来越能胡思乱想，愈发的抑郁。但想想这么持续下去也不是办法，想来想去还是找点事干吧。先充实好自己，总不能说以后机会来临，自己还没准备好。想想我目前也只能干这些了。

之前刷算法题的时候遇到了『树状数组』这种结构，网上大多教程实在是不够通俗，不适合新手（~~但新手并不是自己不会和看不懂的理由~~）。遂仔细研究了一番，有了理解的同时也争取写一份通俗易懂的博客。

问题背景

给定一个数组，和一堆索引[a, b]，求出数组中 a 到 b 区间内的元素和。正常情况下，遍历一次数组并求和的复杂度是 $O(n)$。

在频繁的对区间元素求和的问题中，这样的效率会很低（比如这样的索引对有一万组）；
如果数组内元素也要频繁更新，那么要重新遍历求和。

这种情况下，虽然代码容易编写，但时间复杂度实在太高，这时就引出了树状数组。如果你不能理解问题背景，那么来看一道题。

Problem Description

C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地，Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚，每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手，但这些都逃不过C国的监视。中央情报局要研究敌人究竟演习什么战术，所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人，例如Derek问:“Tidy，马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:”你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救，Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说：”我知错了。。。”但Windbreaker已经挂掉电话了。Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的.

Input

第一行一个整数$T$，表示有$T$组数据。
每组数据第一行一个正整数$N(N<=50000)$，表示敌人有$N$个工兵营地，接下来有$N$个正整数，第$i$个正整数$A_i$代表第$i$个工兵营地里开始时有$A_i$个人$(1<=A_i<=50)$。
接下来每行有一条命令，命令有4种形式：

Add i j，$i$和$j$为正整数，表示第$i$个营地增加$j$个，$j$不超过30；
Sub i j，$i$和$j$为正整数，表示第$i$个营地减少$j$个人，$j$不超过30；
Query i j，$i$和$j$为正整数，$i<=j$，表示询问第$i$到第$j$个营地的总人数；
End 表示结束，这条命令在每组数据最后出现。

每组数据最多有40000条命令。

Output

对第$i$组数据,首先输出“Case i:”和回车；
对于每个Query询问，输出一个整数并回车，表示询问的段中的总人数，这个数保持在int以内。

树状数组

简述

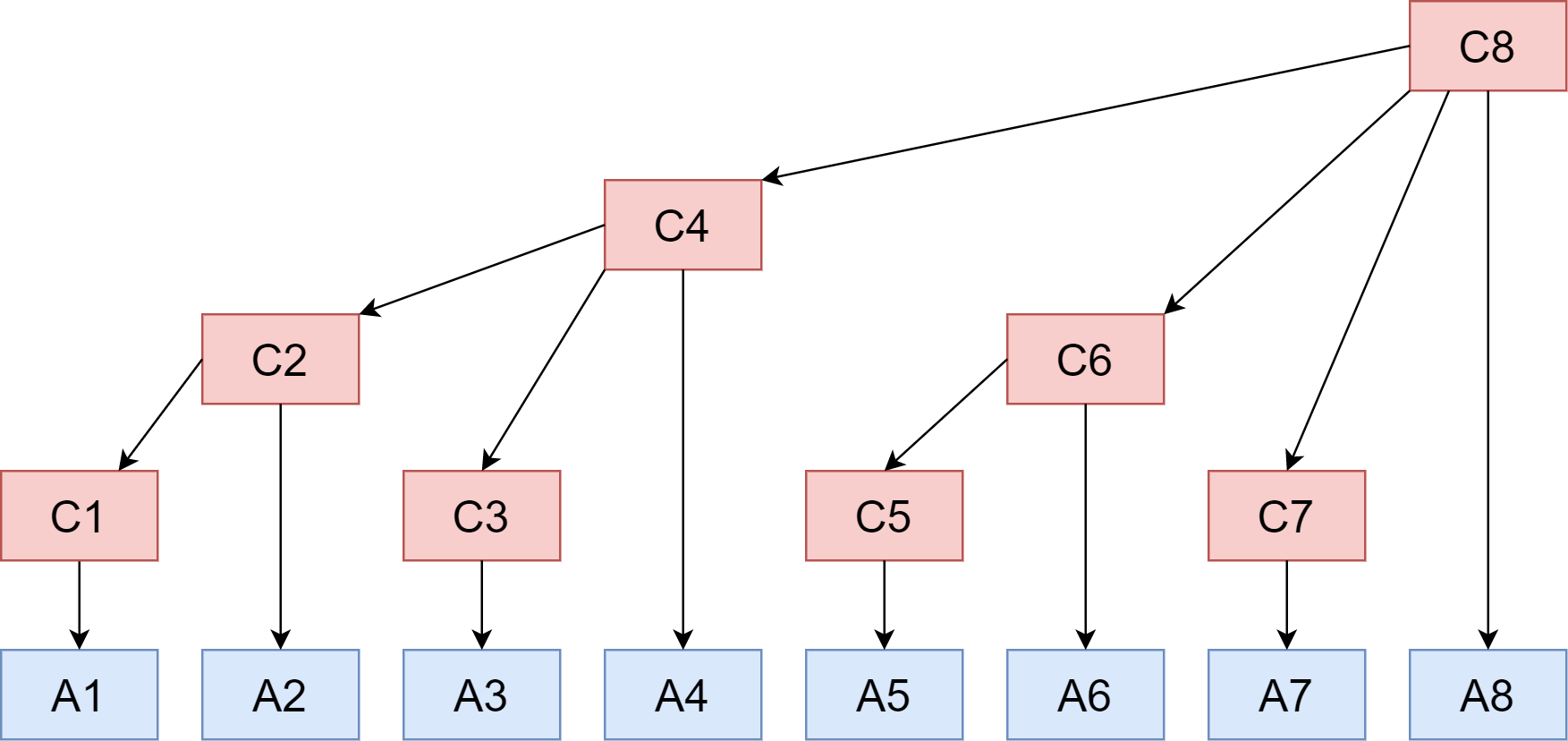
树状数组就长上面那个样子，数组 C 就是树状数组，A 是原数组。这里需要注意的是：

传统的树都有左孩子右孩子，树状数组是没有这些的，只是这个数组的形状像一个树；所以这样的树就不必创建成结点、指针那样的动态树形结构；
求[1, 4]的和，不用求A[1] + A[2] + A[3] + A[4]，直接输出 C[4] 即可；
$i$ 表示数组 C 的索引，十进制；
$j$ 表示数组 A 的索引，十进制。

数组C与数组A的关系

根据上文，我们很容易知道数组 C 是一个对原始数组 A 的预处理数组。观察上图，我们很容易得到下面的表格：

数组 C 索引	数组 C 与数组 A 的关系	数组 C 元素来自数组 A 元素的个数
C[1]	C[1]=A[1]	1
C[2]	C[1]=A[1]+A[2]	2
C[3]	C[1]=A[3]	1
C[4]	C[1]=A[1]+A[2]+A[3]+A[4]	4
C[5]	C[1]=A[5]	1
C[6]	C[1]=A[5]+A[6]	2
C[7]	C[1]=A[7]	1
C[8]	C[1]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]	8

其中：『数组 C 中的元素来自数组 A 的元素个数』，它们的规律如下：将数组 C 的索引 i 表示成二进制。从右向左数，遇到 1 则停止，数出 0 的个数记为 $k$，则计算 $2^k$ 就是『数组 C 中的元素来自数组 A 的个数』。下面举例说明：

当 $i=5$ 时，因为 5 的二进制表示是 0000 0101，从右边向左边数，第 1 个是 1 ，因此 0 的个数是 0，此时 $k=0,2^k=1$，所以 C[5] 只有一个元素 A[5]；
当 $i=8$ 时，因为 8 的二进制表示是 0000 1000，从右边向左边数遇到 1 之前，遇到了 3 个 0，此时 $k=3,2^k=8$，所以 C[5] 由 8 个元素组成。

那么，$2^k$是我们想要的，如何计算呢？这是有公式的：

\begin{equation}
\text{lowbit}(i)=2^k，\text{lowbit}(i) = i \& (-i)
\end{equation}

单点更新

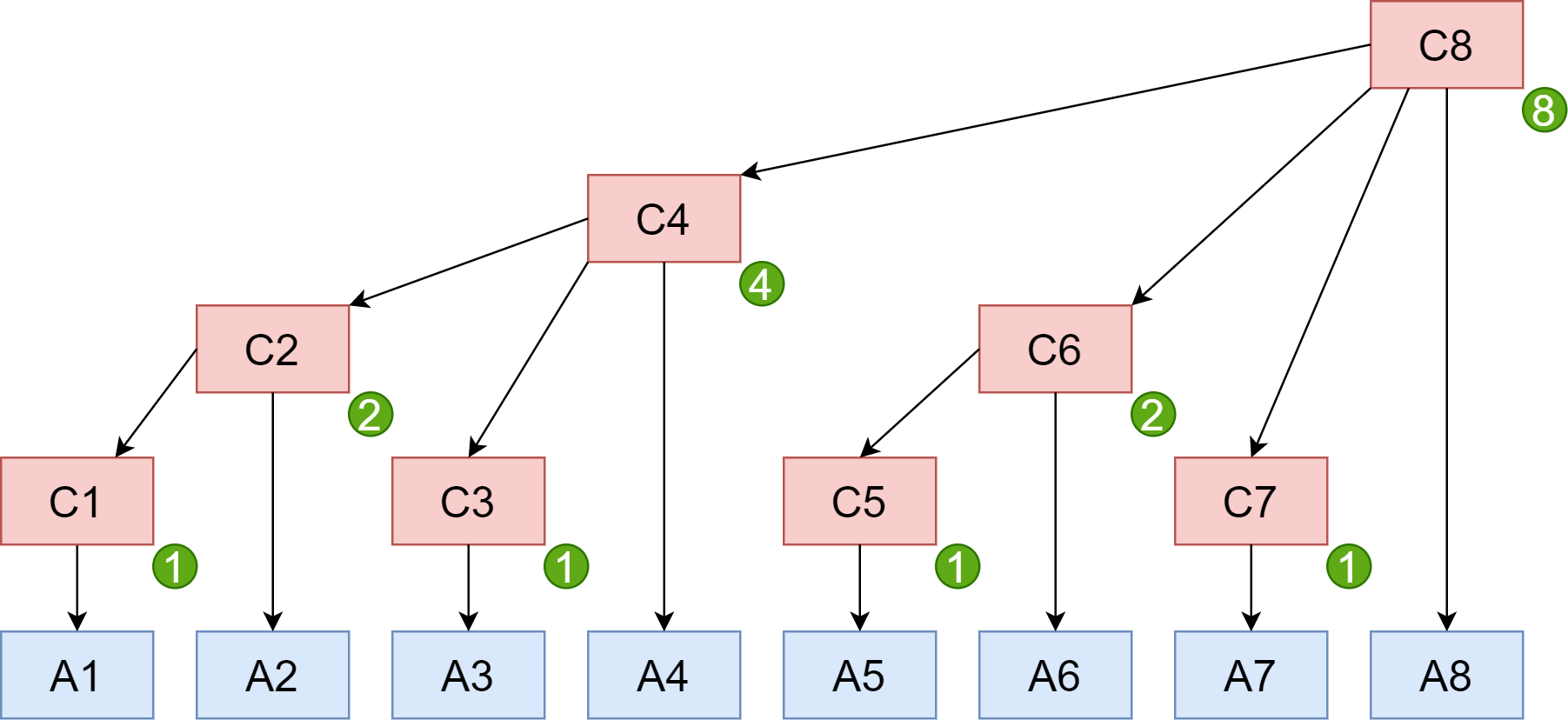
我们在数组 C 每个元素的右下角标注这个元素代表了几个数组 A 中的元素（就是绿色圆圈内的数字）。假设此时我们修改 A[1]，来分析对数组 C 的影响，显而易见，C[1], C[2], C[4], C[8] 的值都要发生改变：

对于 C[1]，$\text{lowbit}(1)=1, 1+\text{lowbit}(1)=2$，得到 C[1] 的父节点索引值 2；
对于 C[2]，$\text{lowbit}(2)=2, 2+\text{lowbit}(2)=4$，得到 C[2] 的父节点索引值 4；
对于 C[4]，$\text{lowbit}(4)=4, 4+\text{lowbit}(4)=8$，得到 C[4] 的父节点索引值 8；

1 即 0001，从右向左，遇到 0 放过，遇到 1 为止，给这个数位加 1。这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 $\text{lowbit}$ 值，马上就发生了进位。得到 0010 ，即 2 的二进制表示。

接下来处理 0010。同样地，这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 $\text{lowbit}$ 值，马上就发发生了进位，得到 0100，即 4 的二进制表示。

然后一直循环下去直到超出数组界限前停止……

由此我们可以总结出规律（并不是规律，而是计算方式导致的）：从已知子结点的索引 $i$ ，则结点 $i$ 的父结点的索引 $\text{parent}$ 的计算公式为：

\begin{equation}
\text{parent}(i)=i+\text{lowbit}(i)
\end{equation}

分析到这里单点更新的伪代码就可以马上写出来了：

int lowbit(int x) {
    return x & (-x);
}

void update(int i, int delta) {
    // len 为数组长度
    while (i <= len) {
        tree[i] += delta;
        i += lowbit(i);
    }
}

区间求和

和单点更新的过程相反，单点更新是通过自己节点索引找出父节点；求和是根据自己节点索引找出子节点，自己和子节点的值相加，就是结果。（理解单点更新就很容易理解区间求和了）

求前四项的和：$\text{lowbit}(4)=4, 4-\text{lowbit}(4)=0$，结果是 C[4] 与前0项的和，（C[0] 默认为 0）；
求前五项的和：$\text{lowbit}(5)=1, 5-\text{lowbit}(5)=4$，结果是 C[5] 与前4项的和；
求前六项的和：$\text{lowbit}(6)=2, 6-\text{lowbit}(6)=4$，结果是 C[6] 与前4项的和；
求前七项的和：$\text{lowbit}(7)=1, 7-\text{lowbit}(7)=6$，结果是 C[7] 与前6项的和；
求前一项的和：$\text{lowbit}(1)=1, 1-\text{lowbit}(1)=0$，结果是 C[1] 与前0项的和。

经过以上分析，也可以很快写出求区间和的伪代码：

int query(int i) {
    // 从右到左查询
    int sum = 0;
    while (i > 0) {
        sum += tree[i];
        i -= lowbit(i);
    }
    return sum;
}

给出文章开头那道题的 AC 代码：

#include <cstdio>
#include <cstring>
#define MAXN 50005
#define lowbit(x) ((x) & (-x))
int tree[MAXN];

void update(int i, int x)
{
    for (int pos = i; pos < MAXN; pos += lowbit(pos))
        tree[pos] += x;
}

int query(int n)
{
    int ans = 0;
    for (int pos = n; pos; pos -= lowbit(pos))
        ans += tree[pos];
    return ans;
}

int main()
{
    int cases;
    scanf("%d", &cases);
    for (int I = 1; I <= cases; ++I)
    {
        memset(tree, 0, sizeof(tree));
        int n, x, a, b;
        char opr[10];
        printf("Case %d:\n", I);
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i)
        {
            scanf("%d", &x);
            update(i, x);
        }
        while (scanf("%s", opr), opr[0] != 'E')
        {
            switch (opr[0])
            {
            case 'A':
                scanf("%d%d", &a, &b);
                update(a, b);
                break;
            case 'S':
                scanf("%d%d", &a, &b);
                update(a, -b);
                break;
            case 'Q':
                scanf("%d%d", &a, &b);
                printf("%d\n",  query(b) - query(a - 1));
            }
        }
    }
    return 0;
}

进阶使用

题目

来看一道实际的题目。来看一下另外的问题背景下如何使用树状数组，源自PAT甲级1057。（如果上文的例子都没有看懂，那么也没必要看这个了，这个更难），先来看题：

Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian — return the median value of all the elements in the stack. With $N$ elements, the median value is defined to be the $(N/2)$-th smallest element if $N$ is even, or $((N+1)/2)$-th if $N$ is odd.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N(≤10^5)$. Then $N$ lines follow, each contains a command in one of the following 3 formats:

1
2
3

Push key
Pop
PeekMedian

where key is a positive integer no more than $10^5$. For each Push command, insert key into the stack and output nothing. For each Pop or PeekMedian command, print in a line the corresponding returned value. If the command is invalid, print Invalid instead.

Sample Input:

17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop

Sample Output:

Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid

常见思路

题目很简单，最简单的想法是：创建数组，压栈弹栈，并排序求出中位数，但显而易见的是，用常见的方法去操作绝对超时（别试了，我试过了）。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector <int> v, m;

int main(int argc, char const *argv[])
{
    int n;
    cin >> n;
    string s;
    for (int i = 0; i < n; i++)
    {
        cin >> s;
        if (s[1] == 'o')
        {
            if (v.empty())
            {
                cout << "Invalid" << endl;
                continue;
            }
            else
            {
                cout << v.back() << endl;
                v.pop_back();
            }
        }
        if (s[1] == 'u')
        {
            int a;
            cin >> a;
            v.push_back(a);
        }
        if (s[1] == 'e')
        {
            if (v.empty())
            {
                cout << "Invalid" << endl;
                continue;
            }
            else
            {
                m.clear();
                m.assign(v.begin(), v.end());
                sort(m.begin(), m.end());
                if (v.size() % 2 == 0) cout << m[v.size() / 2 - 1] << endl;
                else cout << m[(v.size() + 1) / 2 - 1] << endl;   
            }
        }
    }
    return 0;
}

使用树状数组

先理顺下思路，要知道这道题最难的不是压栈和弹栈，而是求出栈内元素的中位数。我们知道了题目的最大长度，那么用 0 初始化对应长度的数组 C 。（注意：数组初始化时不能用变量而应该用常量），初始化代码如下：

1 2	const int maxn = 100005; int c[maxn];

换种角度思考，如果压栈3，那么我们更新 C[3] 及以后的元素，让他们加1；如果压栈6，那么更新 C[6] 及以后的元素，那么最后一个元素 C[maxn-1] 表示栈内元素有几个。单点更新代码如下：

void update(int x, int v) {
    for(int i = x; i < maxn; i += lowbit(i))
        c[i] += v;
}
// x 表示入栈的元素
update(x, 1);

而在求栈内元素中位数时，借助树状数组可以避免排序。可以思考下，按 4, 2, 1, 6, 8 顺序和按 [8, 1, 4, 6, 2] 顺序压入得到的数组 C 是一样的，和 [1, 2, 4, 6, 8]顺序压入得到的 C 也是一样的。那么无论压栈的顺序是如何的，我们都可以认为这种逻辑结构下，元素是顺序压入的。

剩下的就好办了，比如一直到$x$的前缀和就表示：从0一直到$x$，有几个元素。那么简单二分法写一下，临界值是到$\text{mid}$的前缀和与中位数相等，那么输出即可。其实这个问题可以转化为：在数据更新较为频繁、且不能直接排序的情况下，求出一组无序序列的中位数。完整代码如下，left也一定是压入栈内的元素。可以理解为，在顺序序列中，刚好在 left 那使得栈内元素对半分。

#include <iostream>
#include <stack>
#define lowbit(i) ((i) & (-i))
const int maxn = 100010;
using namespace std;
int c[maxn];
stack<int> s;
void update(int x, int v) {
    for(int i = x; i < maxn; i += lowbit(i))
        c[i] += v;
}
int getsum(int x) {
    int sum = 0;
    for(int i = x; i >= 1; i -= lowbit(i))
        sum += c[i];
    return sum;
}
void PeekMedian() {
    int left = 1, right = maxn, mid, k = (s.size() + 1) / 2;
    while(left < right) {
        mid = (left + right) / 2;
        if(getsum(mid) >= k)
            right = mid;
        else
            left = mid + 1;
    }
    printf("%d\n", left);
}
int main() {
    int n, temp;
    scanf("%d", &n);
    char str[15];
    for(int i = 0; i < n; i++) {
        scanf("%s", str);
        if(str[1] == 'u') {
            scanf("%d", &temp);
            s.push(temp);
            update(temp, 1);
        } else if(str[1] == 'o') {
            if(!s.empty()) {
                update(s.top(), -1);
                printf("%d\n", s.top());
                s.pop();
            } else {
                printf("Invalid\n");
            }
        } else {
            if(!s.empty())
                PeekMedian();
            else
                printf("Invalid\n");
        }
    }
    return 0;
}

结语

树状数组就写完了，也不知道自己讲清楚了没有，哪里写的不好可以留言，我在整改。

参考

题目出处：https://zhuanlan.zhihu.com/p/93795692
思想参考（自己做了整改和计算，没有照抄，原文写的也挺不错的）：
https://www.acwing.com/blog/content/80/