因为开发图像检索系统的需要，需要学习局部敏感哈希算法。我在网上看了很多局部敏感哈希算法的讲解，也没有一个能讲清楚的。什么打乱表格、计数 1 最开始出现的索引、minHash 等没啥用的东西把人说的云里雾里。

而如何设计哈希函数、如何把相似内容放到同一个桶中、计算相似度则闭口不谈。所以，关于数学理论推导，本文就不描述了，网上其他博客多的是，本文从代码的角度来理解局部敏感哈希算法，相对更清晰，附 C++ 程序实现。

哈希表

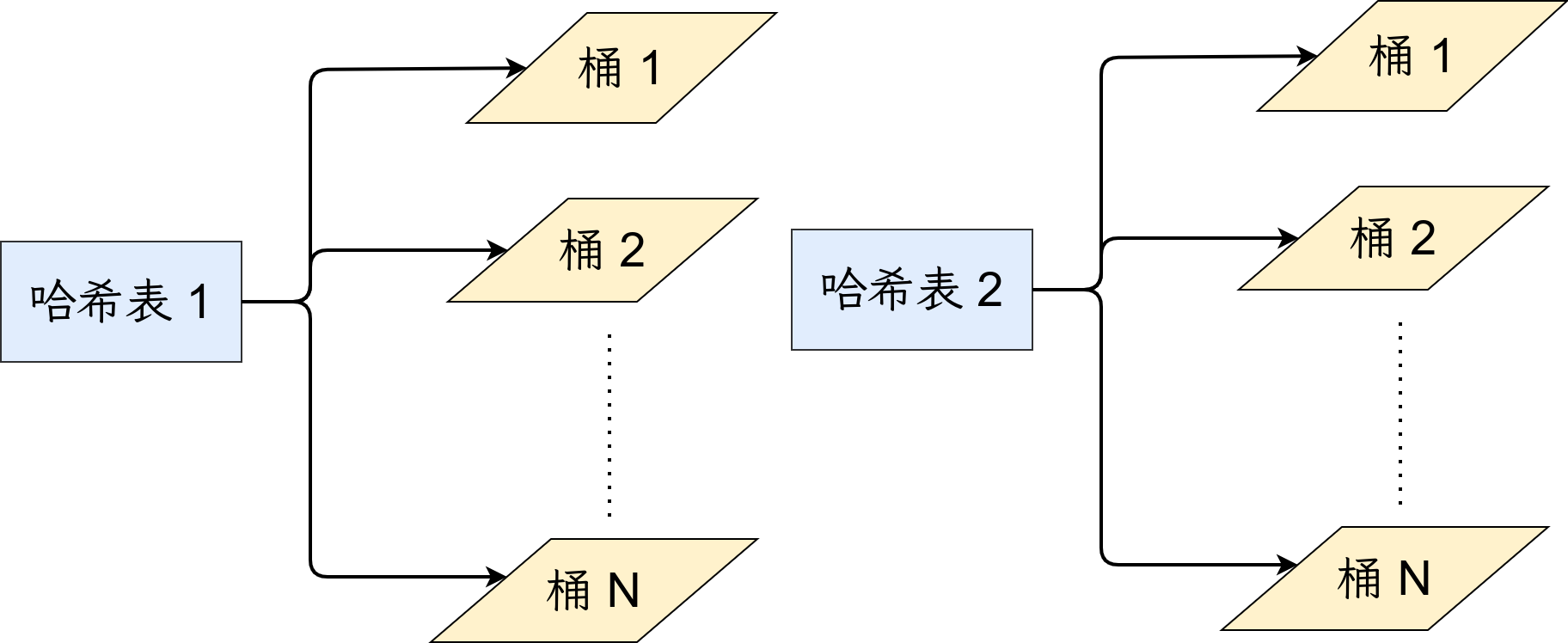
如上图所示有两张不同的哈希表。在查询阶段，对于输入的每条数据，都会在这两个哈希表中进行查询，因此更多的查询结果可以保证查询的召回率。但是，也会带来查询时间、构建哈希表时间线性增加的弊端。会在文末给出如何设置合理的哈希表数目，这里只需要理解哈希表多了、少了的优缺点即可。

在程序中，我们设置哈希表为三维容器，维度为 $T \times 2^{F} \times 0$，$T$ 表示哈希表的数量，$F$ 表示哈希函数的数量，用 $2^F$ 表示桶的数量，$0$ 是每个桶的容量，初始化为 0, 后期桶内添加数据时容量会增加，维度也会随即发生变化。

哈希函数与哈希过程

对于任何局部敏感哈希函数 $f(x)$ 而言，它都应该实现：在处理数据库数据时，相似的特征放入同一个桶，不相似特征放入不同的桶中，每个桶可以有多个结果。在处理查询数据时，同样通过哈希函数 $f(x)$，将当前查询的向量映射到桶中，而后在那个桶中返回最接近的 $K$ 个向量。此时，会触发 $f(x)$ 的隐藏条件，在处理数据库数据和查询数据的时候，$f(x)$ 保持不变。

在程序中，我使用了二级哈希，也就是有两个哈希函数：

一级哈希函数 $f_1$ 是一个二维矩阵，维度是 $T \times F$，每个元素都是 $[0, F)$ 区间内的随机整数。之后会讲述这么做的原因是为了防止越界。
二级哈希函数 $f_2$ 是一个二维矩阵，维度是 $F \times D$，$D$ 是数据的维度数，其元素取值为以 0 为均值，以 0.2 为方差的服从正太分布的随机数。

哈希运算

重点来了，在对数据进行哈希时，按照表、哈希函数、数据维度的顺寻进行三层遍历，程序如下：

// 遍历哈希表
for (int t = 0; t < this->n_tables; t++) {
    // 遍历这些哈希函数
    for (int f = 0; f < this->n_functions; f++) {
        sum = 0;
        for (int i = 0; i < this->n_dim; i++) {
            this->bFile >> x;
            // 一级哈希，this->f_1[t][f]，哈希到某个哈希函数
            // 二级哈希，this->f_2 访问当前哈希函数的第 i 个值
            sum += x * this->f_2[ this->f_1[t][f] ][i];
        }
        if (sum > 0)
            pos += std::pow(2, f);
    }
    if (pos >= std::pow(2, this->n_functions))
        pos = std::pow(2, this->n_functions) - 1;
    // 容器追加，避免处理哈希冲突
    // 追加到第 t 个表的第 pos 个桶中
    this->hashTables[t][pos].push_back(line);

一级哈希 this->f_1[t][f] ，确定使用哪个哈希函数 $i$，因此取值范围是 $[0, F)$
二级哈希，使用第 $i$ 个哈希函数，对当前数据进行哈希，哈希的运算为乘积并求和。这里需要注意的是，「查询数据处理的阶段」和「数据库数据处理阶段」的哈希形式必须一致，否则无法保证查到近似结果。因此，查询阶段的哈希运算也是乘积并求和。
针对哈希结果，确定将当前数据放入哪个桶中，也就是 pos

至于上述程序中为何 sum > 0 和 pos += std::pow(2, f);，都是哈希函数的机制，也可以自己定义新的运算，这个没有统一的标准。

查询阶段

对于查询数据，首先要查找当前数据位于哪个桶，而 pos 的计算和上述的哈希运算完全一致：

int LSH::hash_query(int t, int line) {
  double sum{0}, x{0.0};
  int pos{0};
  for (int i = 0; i < this->n_functions; i++) {
    sum = 0;
    for (int j = 0; j < this->n_dim; j++) {
      this->qFile >> x;
      sum += x * this->hashFunction[this->amplifyFunction[t][i]][j];
    }
    if (sum > 0)
      pos += std::pow(2, i);
  }
  return pos;
}

在获取这个桶后，遍历这个桶内的所有元素，按照相似性距离压入优先级队列，这样就可以逐个访问最相似的元素。

// t 是当前哈希表，pos 是查询到的桶
for (auto& i: this->hashTables[t][pos]) {
    double dis = this->calcute_cosine_distance(i, line);
    // 距离与项，按照第一项进行排序
    this->res.emplace(dis, i);
}

计算相似度

也就是上述程序中的 calcute_cosine_distance 函数，这个还是比较容易实现的。$\text{cos}$ 相似性计算为：

\begin{equation}
\text{sim}= \frac{x \cdot y}{ \Vert x \Vert \Vert y \Vert}
\end{equation}

分子是内积，分母是模长。

关于参数设置

如何确定哈希函数、哈希表的数量呢？

一个极端的假设，我有很多的哈希函数和哈希表，这无疑会增加建立哈希表的复杂度
一个极端的假设，我只有一个哈希函数和一个哈希表，在查询阶段会查询到大量无关的结果

那么，假设数据库里面有 10000 条数据，那么我可以设置 10 个哈希函数，因为 $2^{10}=1024$，这样就有了 1024 个桶。而如果 10000 数据分布均匀，每个桶就可以有 10 条左右的数据，查询也快。至于哈希表，2个，3个都是可以的，但是不能太多。

此外还要注意的是，每个哈希桶内的元素数最好是均匀的，这样查询时间也更稳定。所以要设置合理的哈希函数的机制，也就是 pos 的分布一定要均匀。

程序

我自己实现了一份局部敏感哈希程序，我是 C++ 初学者，代码写的不是很难，相信你看完代码是可以理解局部敏感哈希算法的。计算相似度是使用的余弦距离，因为欧拉距离会面临维灾。modules 里面的 config.cpp 可以忽略，那个是为了衔接其他业务设计的。

性能测试

处理 13466 X 2048 大小的数据，即 13466 条数据，每条数据的维度是 2048 维。构建 1024 个哈希函数，两张哈希表。log 日志显示每秒哈希 50 条数据。对 100 条数据进行查询，每条数据返回最接近的 5 条数据。每条数据的平均查询时间为 0.86 秒，最低时间为 0.34 秒，召回率接 25% 左右。

Just for Life.

从代码角度理解局部敏感哈希算法

哈希表