还是要认真的学习一会儿,降低多巴胺的分泌。在使用 triplet loss 学表示的时候,出现了模型坍塌的情况,也就是说,模型对任何输入的输出都是一样的,损失恒定的现象。在网上搜了一些解决方案后,需要用户去花精力构造正负样本,我不喜欢这样的东西,所以开始看了自监督的论文,毕竟都是学表示。也发现自监督会在一段时间内成为未来的视觉领域的主流,正好我做的东西和自监督也算相关,做一个论文整理。包括了 MoCo,SimCLR,SimSiam 和 Barlow Twins。
模型崩塌,也就是模型为了偷懒,无论什么图片都会输出同样表示,这样结果 loss 很小,然后却没学到任何东西。
图像领域的自监督主要由两部分组成,对比损失和数据增强,而那四篇论文也是基于这两个东西去做的,无非是如何对比。
MoCo
首先是 MoCo,简单的看一下模型的结构
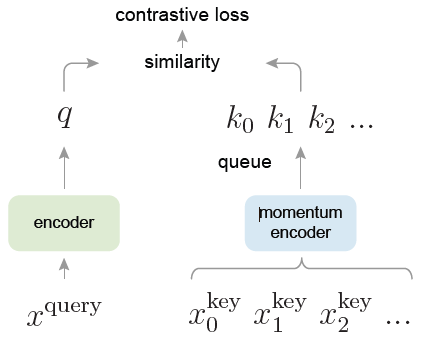
对同一个样本做两次数据增强,会得到两个样本 $x_q$ 和 $x_k$,创建两个 encoder,左边那个 encoder 接入 $x_q$,右边的 encoder 接入 $x_k$,使得这两个的相似性越高越好,与此同时,期望 $x_q$ 与负样本的相似性越低越好。那么如何衡量相似性呢?使用的是 InfoNCE 这个损失函数。
\begin{aligned}
{L}_{InfoNCE} =-{E}_X\left[\log \frac{f_{k}\left(x_{t+k}, c_{t}\right)}{\sum_{x_{j} \in X} f_{k}\left(x_{j}, c_{t}\right)}\right] \\
\end{aligned}
分子是正样本的相似度,分母是负样本的相似度,这个比值越大,log 就越大,对应的损失函数就越小。MoCo 的改动如下,用点积来衡量 $x_q$ 和正负样本的距离。也就是说,使用对比损失来区分图像的高维特征。
\begin{equation}
{L}_q = -\log \frac{ \exp(q\cdot k_{+}/\tau) }{\sum_{i=0}^K \exp(q\cdot k_{i}/\tau)}
\end{equation}
那么与众不同的地方呢?换句话说,负样本从哪里来呢?模型会设计一个队列,队列负责维护将刚进入的样本视为负样本放入队列(最开始没负样本的话,用的是随机数),并弹出之前的负样本,这就需要很大的显存以及代码编写的难度,我不是很喜欢这两点。不信你来看他们官方的程序。
此外需要注意的是,作者提出了动量的更新方式,来更新右侧的网络:
\begin{equation}
\theta_k \leftarrow m\theta_k + (1-m)\theta_q , m\in[0,1)
\end{equation}
也许你会有疑问,都计算好梯度了,更新左侧的网络就没事,更新右侧的网络就有事,莫非在耍流氓?这个梯度给谁不是给,为什么不用梯度更新两个网络?论文上写的是:由于样本很多,右侧网络不容易更新。很多网上的论文解析也是人云亦云,看了代码就知道存储负样本的队列和右侧的网络没半毛钱关系,队列在计算梯度的时候已经 detach 了。所以,论文写的更新困难并不是梯度回传困难,那么为什么不能用梯度更新右侧的网络呢?
先来解释为什么不把左侧网络的参数拷贝给右侧网络的参数。这么做的目的是因为不同 epoch 之间数据分布差异可能很大,encoder 的参数有可能会发生突变,不能将多个 epoch 的数据特征近似成一个静止的大 batch 数据特征,因此就使用了这么一个类似于滑动平均的方法来更新右侧网络。
再来回答为什么不用梯度更新右侧的网络。$x_k$ 经过右侧网络后,然后我们就得到了它们相对应的表示。而对于这个表示,它们不光包含了这个 mini-batch 的表示,也包含了一些之前处理过的 mini-batch 中的表示。换句极端的话说,右侧的网络掌握了全部数据的表示,来调控左侧网络该学到什么样的表示。这些表示通过右侧网络后放入队列中,相对于只在本 mini-batch 内做比较的方法而言,moco 能用较小的管理开销来获得更多的负样本。如果只用一个 mini-batch 的梯度更新右侧网络,或者说右侧网络只掌握一个 mini-batch 的表示,那右侧网络直接输出和左侧网络一样的东西不就行了,这样损失很小,但什么也没学到。因此,不能用一个 mini-batch 的梯度去更新右侧网络。
损失函数解析
此外是本文较为迷惑的损失函数,文章写的没啥迷惑,迷惑的是代码。我第一眼过去,直接理解为不管是正样本还是负样本,都和 0 去接近,正样本明明越大越好,应该和 1 去接近,这么写肯定不对呀。
1 | l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1) |
后来仔细抠的代码才理解,torch 的交叉熵损失函数由 logsoftmax 和 nllloss 组成,前者完成 logsoftmax 的计算,后者 nllloss 取出对应的标签,在 nllloss 的时候,标签为 0 的意思是取出 batch 中的第一列,而这一列正好是正样本,nlloss 期望这列的值越小越好,那么回退到 logsoftmax,就是期望这列的值越大越好,也就是,正样本的相似度很高。并不是像网上那种垃圾博客说的,无监督任务都分成 0 类即可。 这里还是建议理解一下,因为自监督的损失大多是这么设计的。
SimCLR
推荐一个比较好的实现。因为反感 MoCo 那种开显存的操作,毕竟不是所有人都有 facebook 的财力,所以继续去读了其他自监督的论文,较为相似的一篇论文是 SimCLR。还是先来看模型结构图:
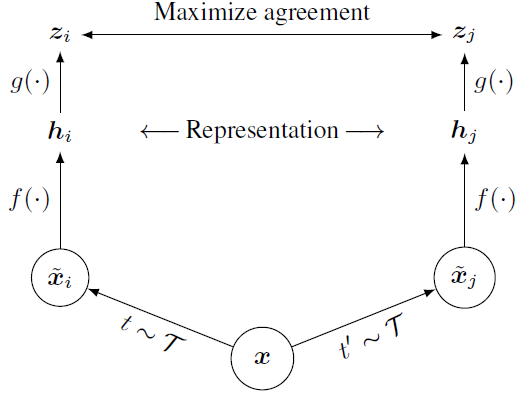
注意,左右两边的网络都是相同的,也就不存在梯度该传给谁的问题。一个 batch 的样本,经过数据增强得到两个 batch 的样本,这两个 batch 的样本进入网络会得到两个 batch 的表示,期待这两组表示中,同一数据的表示很接近,放大不同数据的差异。损失同样是用的类似 InfoNCE 的损失函数。不过论文中有比较奇怪的点,放一段原文:
We randomly sample a minibatch of N examples, augmented examples derived from the minibatch, resulting in 2N data points. We treat the other 2(N-1) augmented examples within a minibatch as negative examples.The final loss is computed across all positive pairs.
问题来了,一共 $2N$ 个样本,$2(N-1)$ 都视为负样本,哪来的 positive pairs?还是直接看代码吧,其实 MoCo 的论文写的也够晕的。看了代码损失函数的设计后发现,就是自己和自己是正样本,自己和其他的样本的关系是负样本。严格来说,对于一个样本而言,有 2(N-2) 个负样本。损失函数和 MoCo 的保持一致,都是用交叉熵损失函数实现的。推荐去看这个损失函数的实现,代码写的还是比较有意思的。但是计算量会大一些。
SimSiam
在 MoCo 之后,提出了更简单的网络结构:
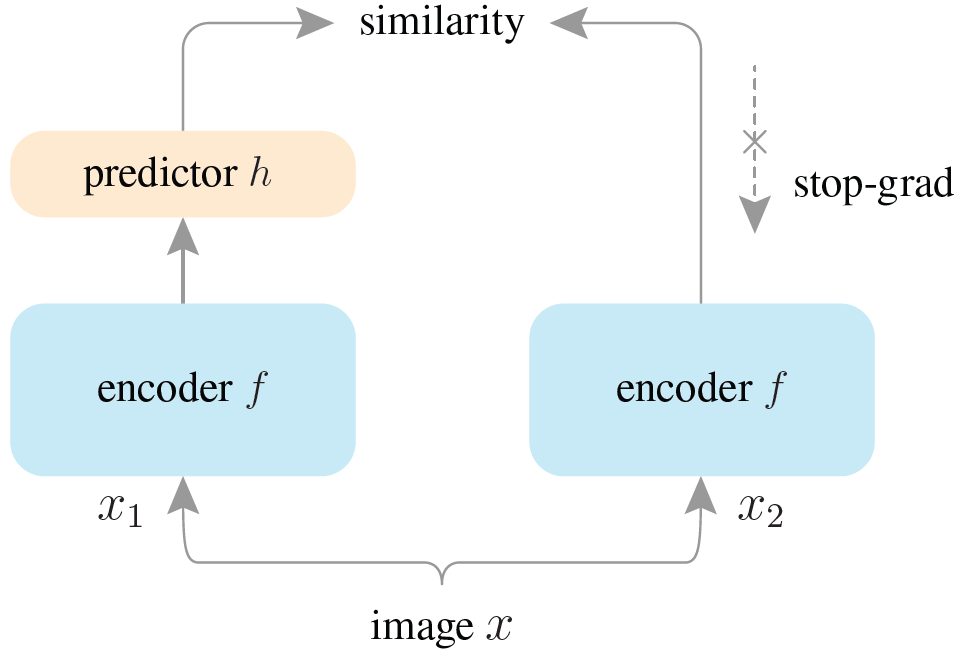
提前声明,相似度用的是余弦函数,因为余弦函数相似性越高数值越大,因此损失函数取了负数,最后的损失值也是负的。思路很简单,对同一个图像做两次增强得到俩个正样本,$x_1$ 和 $x_2$,$x_1$ 经过 encoder 得到表示 $z1$,$z1$ 经过 predictor 得到 $p_1$,同理得到 $p_2$ 和 $z_2$,计算 $p_1$ 和 $z_2$ 以及 $p_2$ 和 $z_1$ 的相似度,然后就没了。
简单吗?简单。有坑吗?有。我当时在想,如果 predictor 的权重全部是 1,那么相似度不就会很小了,但仍然是模型坍塌的情况。然后带着疑问去看代码,结果人家直接冻结了 predictor 某一层的权重,是我大意了。后来我以抄袭的形式复现的时候,没有冻结权重,效果比 SimCLR 要好一些。
Barlow Twins
到这篇论文,思路更加简单,东西和 SimCLR 比较类似,损失函数用的是大二学过的协方差矩阵,对角线越大越好,其余位置越小越好。它虽然很简洁,但我感觉他比 SimSiam 更令人喜欢。
\begin{equation}
L=\sum_{i}(1-C_{ii})^2 + \lambda \sum_i \sum_{j\neq i} C_{ij}^2
\end{equation}

