Just for Life.

明月更几时

0%

算法系列：区间问题

发表于 更新于
本文字数： 6.3k 阅读时长 ≈ 6 分钟

算法继续整理系列之区间问题。这类问题可以总结或者变化为：给定多个区间，求满足覆盖范围的最小相交区间的数量。一般而言都是：题目给定一个乱序的区间。我们需要对区间进行排序调整和统计结果，来满足题目条件。其中变化的部分只有如何处理相交区间，因此整理一个通用的算法模板。

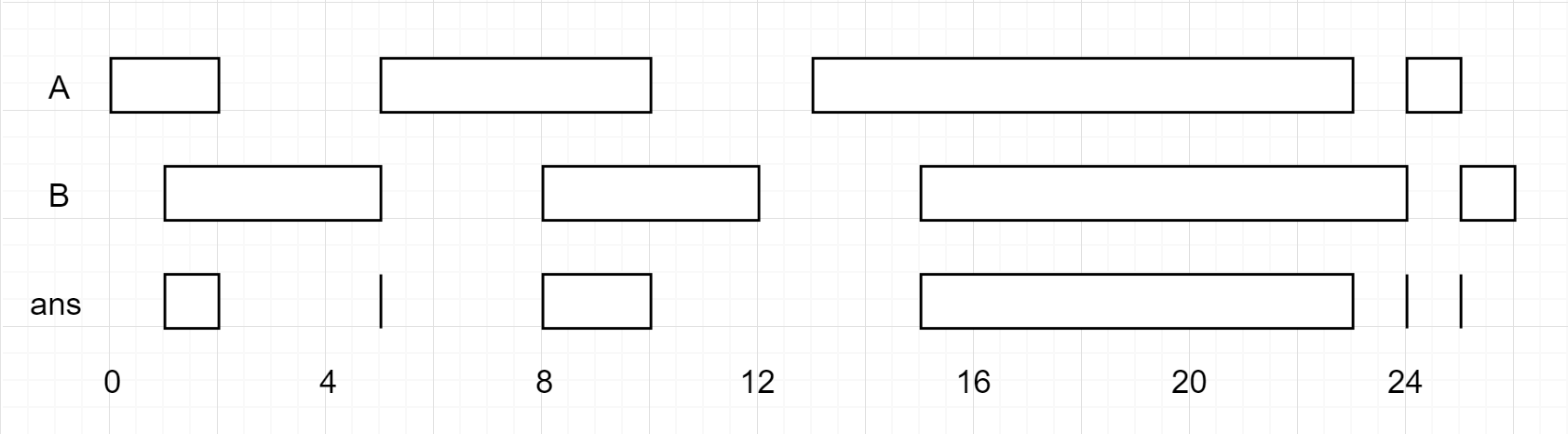
区间固定

986. 固定区间的交集

先看一道简单的题目，这个题目中我们不需要对区间进行排序调整，因此相对简单一些。

这个题目很简单，我们只需要按照顺序遍历区间，处理相交部分：

  1. 判断两个区间是否相交，如果不相交，右侧区间靠前的那一组，索引向后移动
  2. 如果相交，取出交集，右侧区间靠前的那一组，索引向后移动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        int i = 0, j = 0;
        vector<vector<int>> res;
        while (i < firstList.size() && j < secondList.size()) {
            int l1 = firstList[i][0];
            int r1 = firstList[i][1];
            int l2 = secondList[j][0];
            int r2 = secondList[j][1];
            // 没有交集
            if (l1 > r2 || r1 < l2) {
                // r2 比较小，为了尽快和 l1 相交，需要向后移动
                if (l1 > r2) {
                    j++;
                } else {
                    i++;
                }
                continue;
            }
            int a = max(l1, l2);
            int b = min(r1, r2);
            // 交集
            res.push_back({a, b});
            if (r2 > r1) {
                i++;
            } else {
                j++;
            }
        }
        return res;
    }
};

区间可变

代表题目：1288 删除覆盖区间，56 合并区间，452 射箭引爆气球，1024 视频拼接 和 435 无重叠区间。

1288. 删除覆盖区间

1
2
3
输入：intervals = [[1,4],[3,6],[2,8]]
输出：2
解释：区间 [3,6] 被区间 [2,8] 覆盖，所以它被删除了。

题目意思比较明确，删除大区间覆盖的小区间，那么如何统计被覆盖的区间呢？我们看来看图：

如果想统计一个区间覆盖更多的区间，乱序状态下用暴力算法肯定是可以破解的，大不了一个一个统计。但是如果我们对区间排序一下，按照左侧区间升序或者右侧区间降序，问题会简单很多：

以按照左侧区间排序为例，排序结果如图 (c) 中所示的三种情况：

  • 如果是覆盖的相交情况，统计数量
  • 如果相交的情况，表示上面区间没有能力覆盖下面的区间了，不再考虑上面的区间，开始往下移动
  • 如果没有重叠也就是不相交，同样表示上面区间没有能力覆盖下面的区间了，不再考虑上面的区间

图(a)是按照左侧的区间升序，我们只需要顺序遍历区间，依次判断上面的区间的右侧值是否能覆盖下面的区间的右侧值即可，因为左侧区间已经排好序了，是肯定能覆盖的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[0] == b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }

    int removeCoveredIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        int r = intervals[0][1];
        int cnt = 0;
        for (int i = 1; i < intervals.size(); i++) {
            // 相交时的处理
            if (r >= intervals[i][1]) {
                cnt ++;
            }
            // 没有覆盖，向后移动
            else {
                r = intervals[i][1];
            }
        }
        return intervals.size() - cnt;
    }
};

同理，图(b)是我们按照右侧区间降序排列，此时统计上一个左侧区间能覆盖下一个左侧区间的数量即可，因为右侧区间肯定能覆盖。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[1] == b[1])
            return a[0] < b[0];
        return a[1] > b[1];
    }

    int removeCoveredIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        int l = intervals[0][0];
        int cnt = 0;
        for (int i = 1; i < intervals.size(); i++) {
            if (l <= intervals[i][0]) {
                cnt ++;
            }
            else {
                l = intervals[i][0];
            }
        }
        return intervals.size() - cnt;
    }
};

56. 合并区间

1
2
3
输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

至此，leetcode 的第 56 题区间合并也可以轻松写出程序。思路和覆盖是一样的：

  • 如果上一个区间覆盖了下一个区间，那么合并区间，也就是相交区间的处理
  • 如果上一个区间没有覆盖下一个区间，那么从头开始
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:

    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[0] == b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }

    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        int r = intervals[0][1];
        int l = intervals[0][0];
        vector<vector<int>> res;
        for (int i = 1; i < intervals.size(); i++) {
            // 相交处理，合并
            if (r >= intervals[i][0]) {
                l = min(l, intervals[i][0]);
                r = max(r, intervals[i][1]);
            } else {
                // 不能覆盖，先把之前的结果添加进来
                // 并重新更新区间
                res.push_back({l, r});
                l = intervals[i][0];
                r = intervals[i][1];
            }
        }
        // 最后一组没有被添加进来
        res.push_back({l, r});
        return res;
    }
};

452. 用最少数量的箭引爆气球

1
2
3
4
5
输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

只需要对区间排序，每次统计相交区间的交集，直到交集没有重叠时，射箭数量需要加一。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:

    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[0] == b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }

    int findMinArrowShots(vector<vector<int>>& points) {
        sort(points.begin(), points.end(), cmp);
        int l = points[0][0];
        int r = points[0][1];
        int cnt = 0;
        for (int i = 1; i < points.size(); i++) {
            if (r < points[i][0]) {
                cnt++;
                l = points[i][0];
                r = points[i][1];
            } else {
                // 相交处理，有相交区间，缩小相交区间
                l = max(l, points[i][0]);
                r = min(r, points[i][1]);
            }
        }
        return cnt + 1;
    }
};

435. 无重叠区间

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

1
2
3
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

注意，这个题目和之前的题目不太相同，具体体现在相交时的处理，而相交分为覆盖和非覆盖：

  1. 如果上一个区间覆盖了下面的区间，说明上面的区间太大了。由于我们要删除最少数量的区间，因此首先考虑删除覆盖更广的区间
  2. 如果上一个区间和下一个区间相交，此时不能像之前的合并、相交一样，直接移动到下一个区间或处抛弃上面的区间。因为区间在排序后，如果上一个区间和第二个区间相交，上一个区间和第三个区间不相交，此时我们要删除第二个区间，而不是上一个和第三个区间。因此，相交时我们应该保留上一个区间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[0] == b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), cmp);
        int r = intervals[0][1];
        int l = intervals[0][0];
        int cnt = 0;
        for (int i = 1; i < intervals.size(); i++) {
            // 覆盖，往下移动
            if (l <= intervals[i][0] && r >= intervals[i][1]) {
                cnt ++;
                l = intervals[i][0];
                r = intervals[i][1];
            } else if (r > intervals[i][0]) {
                // 相交，不移动，保留上一个区间
                cnt++;
            } else {
                // 不相交，往后移动，看看后面有多少相交的要处理
                r = intervals[i][1];
            }
        }
        return cnt;
    }
};

1024. 视频拼接

你将会获得一系列视频片段，这些片段来自于一项持续时长为 time 秒的体育赛事。这些片段可能有所重叠，也可能长度不一。我们需要将这些片段进行再剪辑，并将剪辑后的内容拼接成覆盖整个运动过程的片段（[0, time]）。返回所需片段的最小数目，如果无法完成该任务，则返回 -1 。

1
2
3
4
5
6
7
输入：clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10
输出：3
解释：
选中 [0,2], [8,10], [1,9] 这三个片段。
然后，按下面的方案重制比赛片段：
将 [1,9] 再剪辑为 [1,2] + [2,8] + [8,9] 。
现在手上的片段为 [0,2] + [2,8] + [8,10]，而这些覆盖了整场比赛 [0, 10]。

从题面上我们能看出来：在多个片段相交的基础上，我们尽可能选择时间长的片段，这样才能使用的碎片最少。同样，重点就在于：相交时，我们要选择最长的片段。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    static bool cmp(vector<int>& a, vector<int>& b) {
        if (a[0] == b[0])
            return a[1] > b[1];
        return a[0] < b[0];
    }
    int videoStitching(vector<vector<int>>& clips, int time) {
        sort(clips.begin(), clips.end(), cmp);
        int l = 0, r = 0, i = 0, cnt = 0;
        // 从起点开始
        while (i < clips.size() && clips[i][0] <= l) {
            // 碎片部分和起点相交，选择片段最长的
            while (i < clips.size() && clips[i][0] <= l) {
                r = max(clips[i][1], r);
                i++;
            }
            cnt++;
            if (r >= time)
                return cnt;
            // 最长的片段，是下个片段的起点
            l = r;
        }
        return -1;
    }
};

参考

更像是把 labuladong 上区间的题目整理到了一起，写出自己风格的代码。

本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章