Just for Life.

明月更几时

0%

算法系列：回溯

发表于 更新于
本文字数： 12k 阅读时长 ≈ 11 分钟

回溯算法是一种暴力枚举的算法。但是，枚举是一个技术活，枚举过程如何保证不重复、剪纸、不遗漏和优先处理可能的结果，这并不简单。

回溯应该是算法系列中除动态规划外最难的一个，需要很好的明确回溯入口，退出条件，两者保证回溯的不遗漏。而下一步如何回溯，以及如何退出当前状态要保证回溯的不重复。也许有些抽象，我们来看具体例子。

什么是回溯

如果简单的说回溯，那么如下函数就可以解释清楚：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for (auto i : arr) {
    backtrack(i);
}
void backtrack(int i) {
    if (i > n)
        退出条件
    // 回溯入口
    for (auto j : arr[i]) {
        vector.push_back(j);
        // 下一步而回溯
        backtrack(j);
        // 退出当前的状态，往回走
        // 因此叫做回溯
        vector.pop_back()
    }
}

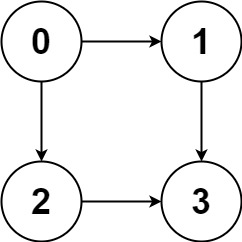
图路径

797. 所有可能的路径

给你一个有 n 个节点的 有向无环图 DAG，请你找出所有从节点 0 到节点 n-1 的路径并输出，不要求按特定顺序。graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

1
2
3
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

如果说从 0 开始，而 0 又指向 1 和 2，那么只能按照这样的顺序找下去，因为题目并没有说要求最短路径。如果遍历的是 0，1，3，那么在找完这条路径后，需要回退，找到 0，1，2 这条路径。也就是，这算是一道回溯类题目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        tmp.push_back(0);
        int n = graph.size();
        // 回溯入口
        dfs(0, n, graph);
        return res;
    }

    void dfs(int idx, int n, vector<vector<int>>& graph) {
        // 退出条件
        if (idx >= n - 1) {
            res.push_back(tmp);
            return;
        } else {
            // 回溯入口
            for (auto i : graph[idx]) {
                tmp.push_back(i);
                dfs(i, n, graph);
                // 回溯
                tmp.pop_back();
            }
        }
    }
};

排列问题

46. 全排列

给定一个不含重复数字的数组 nums，返回其所有可能的全排列 。你可以按任意顺序返回答案。示例：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

和上一题大体相同，我们来分析一下不同点在哪里。

  • 全排列问题，由于会出现 [3,2,1] 这样的情况，因此回溯的入口每次都是 0，而不能是上次回溯的终点，因为 3 后面没有任何东西
  • 其次，由于每次入口都是 0，而且每个元素只能出现一次，因此我们需要使用一个 map，根据索引记录该元素是否使用，只有没有使用时才能回溯
  • 回溯的退出条件为子序列长度等于 nums 的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    unordered_map<int, int> m;
    vector<vector<int>> permute(vector<int>& nums) {
        backtrack(0, nums);
        return res;
    }

    void backtrack(int idx, vector<int>& nums) {
        if (tmp.size() == nums.size()) {
            res.push_back(tmp);
            return;
        } else {
            for (int i = 0; i < nums.size(); i++) {
                if (m[i] == 0) {
                    tmp.push_back(nums[i]);
                    m[i] = 1;
                    backtrack(i, nums);
                    m[i] = 0;
                    tmp.pop_back();
                }
            }
        }
    }
};

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。示例：

1
2
3
4
5
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

根据前面提到的求解回溯问题的框架，我们可以注意到这个题有两个细节：

  • 由于 2 可以出现在 1 的前面，因此每次回溯的起点都是 0。而为了避免添加重复元素，我们需要使用一个 map，记录哪些元素被添加过，从过跳过已经被添加的元素
  • 由于会有重复元素，根据我对回溯问题的了解，我建议先对 nums 进行排序，而后先将结果添加到集合内，最后将结果放入 vector 内
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    unordered_map<int, int> m;
    vector<int> tmp;
    set<vector<int>> res;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        backtrack(0, nums);
        vector<vector<int>> r;
        for (auto i : res)
            r.push_back(i);
        return r;
    }

    void backtrack(int idx, vector<int>& nums) {
        if (tmp.size() == nums.size()) {
            res.insert(tmp);
            return ;
        } else {
            // 回溯入口始终为 0
            for (int i = 0; i < nums.size(); i++) {
                // 如果没有被添加
                if (m[i] == 0) {
                    tmp.push_back(nums[i]);
                    m[i] = 1;
                    backtrack(0, nums);
                    m[i] = 0;
                    tmp.pop_back();
                }
            }
        }
    }
};

组合问题

39. 组合总和

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合 ，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。对于给定的输入，保证和为 target 的不同组合数少于 150 个。

1
2
3
4
5
6
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

需要注意的是，如果回溯的入口是 0，那么可以得到 2+2+3=7 的结果，在后续的回溯中，如果入口是 1，而 3 在之前以及的结果中已经使用过了。因此和上一题不一样的是，下一次回溯的入口是上一次回溯的出口，由于一个数值允许多次使用，因此入口和出口的值是可以相等的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    map<vector<int>, int> m;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtrack(0, candidates, target);
        return res;
    }

    int _sum(vector<int>& tmp) {
        int s = 0;
        for (auto i : tmp)
            s += i;
        return s;
    }

    void backtrack(int idx, vector<int>& candidates, int target) {
        if (_sum(tmp) == target) {
            res.push_back(tmp);
            return ;
        } else {
            // idx 是回溯的入口
            for (int i = idx; i < candidates.size(); i++) {
                if ((candidates[i] <= target) && (_sum(tmp) + candidates[i] <= target)) {
                    tmp.push_back(candidates[i]);
                    // i 是回溯的出口，也就是下一次回溯的入口
                    backtrack(i, candidates, target);
                    tmp.pop_back();
                }
            }
        }
    }
};

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。注意：解集不能包含重复的组合。示例 :

1
2
3
4
5
6
7
8
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
  • 既然每个数字只能使用一次，根据上一题我们能知道：下一次回溯的入口和上一次回溯的出口不能相同
  • 此外，这个题的重点是：可能存在相同数字，因此，我们需要在回溯的过程中进行剪枝。剪枝发生在：同一层数值相同的结点第 2、3 … 个结点，因为数值相同的第 1 个结点已经搜索出了包含了这个数值的全部结果，同一层的其它结点，候选数的个数更少，搜索出的结果一定不会比第 1 个结点更多，并且是第 1 个结点的子集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:

    set<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        int tmp_sum = 0;
        sort(candidates.begin(), candidates.end());
        backtrack(0, tmp_sum, candidates, target);
        vector<vector<int>> r1;
        for(auto i : res) {
            r1.push_back(i);
        }
        return r1;
    }

    void backtrack(int idx, int& tmp_sum, vector<int>& candidates, int target) {
        if (tmp_sum == target) {
            res.insert(tmp);
            return;
        } else {
            for (int i = idx; i < candidates.size(); i++) {
                // 剪枝，i > idx 保证第一个结果计算完了
                // candidates[i] == candidates[i-1] 去除相同的子情况
                if (i > idx && candidates[i] == candidates[i-1])
                    continue;
                if (tmp_sum + candidates[i] <= target) {
                    tmp.push_back(candidates[i]);
                    tmp_sum += candidates[i];
                    backtrack(i + 1, tmp_sum, candidates, target);
                    tmp_sum -= candidates[i];
                    tmp.pop_back();
                }
            }
        }
    }
};

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按任何顺序返回答案。示例：

1
2
3
4
5
6
7
8
9
10
输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]
  • 由于出现 [1,2] 后就不会在出现 [2,1]，因此每次回溯的入口是上次回溯的出口 +1
  • 回溯的退出条件是 tmp.size()==k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> tmp;
    vector<vector<int>> res;
    vector<vector<int>> combine(int n, int k) {
        backtrack(1, n, k);
        return res;
    }

    void backtrack(int idx, int n, int k) {
        if (tmp.size() == k) {
            res.push_back(tmp);
            return ;
        } else {
            for (int i = idx; i <= n; i++) {
                tmp.push_back(i);
                // 下一次回溯的入口，是本次回溯出口 +1
                backtrack(i + 1, n, k);
                tmp.pop_back();
            }
        }
    }
};

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字 1 到 9
  • 每个数字最多使用一次
  • 返回所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例:

1
2
3
4
5
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
  • 由于每个数字只能使用一次，因此每次回溯的入口是上次回溯的出口 +1
  • 回溯退出的条件有两个，一个是和满足，一个是数量满足
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> combinationSum3(int k, int n) {
        int tmpSum = 0;
        backtrack(1, k, n, tmpSum);
        return res;
    }

    void backtrack(int idx, int k, int n, int& tmpSum) {
        if (tmpSum == n && tmp.size() == k) {
            res.push_back(tmp);
            return; 
        } else {
            for (int i = idx; i <= 9; i++) {
                if (tmpSum + i <= n) {
                    tmp.push_back(i);
                    tmpSum += i;
                    backtrack(i + 1, k, n, tmpSum);
                    tmpSum -= i;
                    tmp.pop_back();
                }
            }
        }
    }
};

子集问题

78. 子集

给你一个整数数组 nums，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。你可以按任意顺序返回解集。示例：

1
2
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

我们发现回溯期间的任何结果都会被返回，即使是一个空集，因此：回溯不在设置退出条件，但此时需要保证回溯的入口条件正确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(0, nums);
        return res;
    }

    void backtrack(int idx, vector<int>& nums) {
        res.push_back(tmp);
        for (int i = idx; i < nums.size(); i++) {
            tmp.push_back(nums[i]);
            backtrack(i + 1, nums);
            tmp.pop_back();
        }
    }
};

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。示例：

1
2
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

前文已经提到过，如果有重复元素，对于重复元素，先排序，在将结果存储到集合中，最后转化为 vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    set<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        backtrack(0, nums);
        vector<vector<int>> r;
        for (auto i : res) {
            r.push_back(i);
        }
        return r;
    }

    void backtrack(int idx, vector<int>& nums) {
        res.insert(tmp);
        for (int i = idx; i < nums.size(); i++) {
            tmp.push_back(nums[i]);
            backtrack(i + 1, nums);
            tmp.pop_back();
        }
    }
};

回溯实战

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。示例：

1
2
输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

这个和之前的回溯还不太一样，之前的回溯是选择填入一个数字，或者说每次回溯只能选择一个数字，而一般是可以按照顺序选择数字的。但是这个题不同的是，当前的字符取决于前面的字符，如果前面的字符是 (，那么后面的字符可能是 ( 或者 )，如果前面的字符是 )，后面的字符可能是 ( 或 )，具体是哪一个还需要判断前面的次数，这样程序的逻辑会很复杂。

也就是说，这种情况，不能用 for 循环遍历 () 来回溯。既然如此，只能在回溯中进行遍历。

  • 如果此时任何一个括号的使用次数大于 n，退出
  • 回溯期间，无论如何左括号的使用次数一定大于右括号，因此当右括号的使用次数大于左括号时，退出
  • 之后就是没有循环的回溯，回溯有两部分，分别是添加 ( 和 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    string s{""};
    vector<string> res;
    vector<string> generateParenthesis(int n) {
        backtrack(n, n);
        return res;
    }

    void backtrack(int l, int r) {
        if (l < 0 || r < 0)
            return;
        if (r < l)
            return;
        // 所有括号被添加
        if (l == 0 && r == 0) {
            res.push_back(s);
            return;
        }
        // 追加左括号
        s += "(";
        backtrack(l - 1, r);
        s.pop_back();
        // 追加右括号
        s += ")";
        backtrack(l, r - 1);
        s.pop_back();
    }
};

回溯游戏

37. 解数独

编写一个程序，通过填充空格来解决数独问题。数独的解法需遵循如下规则：

  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
  • 数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

  • 对于这个回溯问题，我们发现遍历时有三种状态：行、列和数字，也就是说，不同于之前的数组遍历，选择一个数字就行。这个题在遍历期间，需要处理三种状态。
  • 一般情况是，回溯本身就能处理一些状态的遍历，此时需要保证本次回溯的入口是上次回溯的出口 +1。
  • 对于本题目，回溯本身处理行和列的遍历，每次回溯时列自增，当列等于 9 时行自增。而在回溯中，使用训练遍历数字，由于上一个回溯选择数字和本次回溯选择的数字有先后关系，因此数字的循环始终为 1,...,9。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        dfs(0, 0, board);
    }

    bool isvalid(char c, int row, int col, vector<vector<char>>& board) {
        for (int i = 0; i < 9; i++) {
            if (board[i][col] == c) return false;
            if (board[row][i] == c) return false;
            if (board[(row/3)*3 + i/3][(col/3)*3 + i%3] == c)
                return false;
        }
        return true;
    }

    bool dfs(int row, int col, vector<vector<char>>& board) {
        if (row < 0 || col < 0 || row > 9 || col > 9) {
            return false;
        }
        if (col == 9) {
            return dfs(row + 1, 0, board);
        }
        if (row == 9) {
            return true;
        }
        if (board[row][col] != '.') {
            return dfs(row, col + 1, board);
        }
        for (char c = '1'; c <= '9'; c++) {
            if (isvalid(c, row, col, board)) {
                board[row][col] = c;
                if (dfs(row, col + 1, board))
                    return true;
                board[row][col] = '.';
            }
        }
        return false;
    }
};

51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 Q 和 . 分别代表了皇后和空位。

和数独不一样的是，这个题的遍历状态只有行和列，因为棋子的状态只有 Q，回溯前放 Q，回溯后回退为 . 即可。

既然如此，按照常规的想法，就用循环遍历列，当这一列满足要求时，就进入下一行，开始填充下一行的棋子，想到这里，回溯的程序也就可以写出来了。

也就是说对于回溯问题，至少要让回溯中的循环控制一个状态的遍历，而回溯本身则控制其他状态的遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
public:
    vector<vector<string>> res;
    vector<string> tmp;
    vector<vector<string>> solveNQueens(int n) {
        tmp.resize(n);
        for (int i = 0; i < n; i++) {
            string s = "";
            for (int i = 0; i < n; i++)
                s += '.';
            tmp[i] = s;
        }
        backtrack(0, tmp);
        return res;
    }

    bool valid(int row, int col, vector<string>& tmp) {
        for (int i = 0; i < tmp.size(); i++) {
            if (tmp[row][i] == 'Q')
                return false;
        }
        for (int i = 0; i < tmp.size(); i++) {
            if (tmp[i][col] == 'Q')
                return false;
        }
        for (int i = row - 1, j = col - 1; ((i >= 0) && (j >= 0)); i--, j--) {
            if (tmp[i][j] == 'Q')
                return false;
        }
        for (int i = row - 1, j = col + 1; ((i >= 0) && (j < tmp.size())); i--, j++) {
            if (tmp[i][j] == 'Q')
                return false;
        }
        return true;
    }

    void backtrack(int row, vector<string>& tmp) {
        if (row < 0)
            return;
        if (row == tmp.size()) {
            res.push_back(tmp);
            return;
        }
        for (int i = 0; i < tmp.size(); i++) {
            if (valid(row, i, tmp)) {
                tmp[row][i] = 'Q';
                backtrack(row + 1, tmp);
                tmp[row][i] = '.';
            }
        }
    }
};
本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章