Just for Life.

明月更几时

0%

算法系列：优先遍历

发表于 更新于
本文字数： 4.9k 阅读时长 ≈ 4 分钟

主要收录深度优先遍历和宽度优先遍历，深度优先遍历一般可以与回溯、递归、树等方法联用，达到优雅遍历的效果，而宽度优先搜索可以用到最短路问题的求解中。

  • 为什么不用 bfs 去遍历？第一是因为 bfs 写起来麻烦，不如 dfs 直观。第二是在某些查找到满足情况即可退出的应用而言，bfs 需要一层一层的去检查，效率很低。
  • 为什么不用 dfs 去求最短路？如上所示，bfs 可以一层一层的检查，相对 dfs 更容易查到最短路。

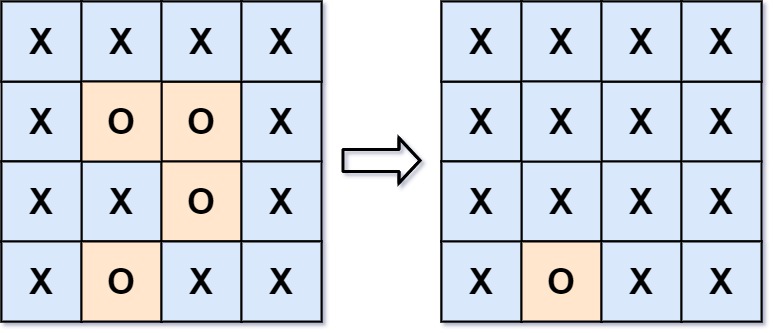
dfs

岛屿问题

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

  1. 那么如何填充内部的 O 呢？这里就要用到 dfs，首先遍历 board，如果遇到了 O，那个和这个 O 相邻的 O 也要被填充，此时就要使用 dfs 来查找相邻的 O
  2. 由于只填充被 X 包围的 O，因此，边界上的 O 不能被填充。那么我们预先把和边界相连的 O 都填充为其他符号，在处理完 board 内部的 O 的时候，在把其他符号替换为 O 即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int n, m;
    void solve(vector<vector<char>>& board) {
        n = board.size();
        m = board[0].size();
        // 替换边界
        for (int i = 0; i < n; i++) {
            dfs(i, 0, board, '+');
            dfs(i, m-1, board, '+');
        }
        for (int i = 0; i < m; i++) {
            dfs(0, i, board, '+');
            dfs(n-1, i, board, '+');
        }
        // 填充内部的 O
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'O') {
                    dfs(i, j, board, 'X');
                }
            }
        }
        // 替换回来
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == '+') {
                    board[i][j] = 'O';
                }
            }
        }
    }

    // dfs 查找相连的 O
    void dfs(int r, int c, vector<vector<char>>& board, char pad) {
        if (r < 0 || c < 0 || r >= n || c >= m) {
            return;
        }
        if (board[r][c] == 'O') {
            board[r][c] = pad;
            dfs(r + 1, c, board, pad);
            dfs(r - 1, c, board, pad);
            dfs(r, c + 1, board, pad);
            dfs(r, c - 1, board, pad);
        }
    }
};

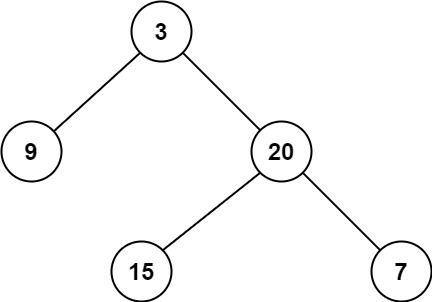
bfs

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明：叶子节点是指没有子节点的节点。

求二叉树或者多叉树中根节点到叶子节点的最短路径，一般都是 bfs 遍历算法。给出 bfs 的模板：

1
2
3
4
5
6
7
8
9
10
11
12
queue.push(root);
while (queue.size()) {
    int s = queue.size();
    for (int i = 0; i < s; i++) {
        auto node = queue.top();
        queue.pop();
        if (node->left != null)
            queue.push(node->left);
        if (node->right != null)
            queue.push(node->right);
    }
}
  • 在进入 bfs 之前先处理一些极端的特殊情况，比如根节点为空，根节点就是目标节点等
  • 在处理完特殊情况后，之后就是 bfs 遍历，如果遍历期间的节点满足目标情况，返回结果即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if (root == nullptr)
            return 0;
        if (root->left == nullptr && root->right == nullptr)
            return 1;
        int depth = 1;
        deque<TreeNode*> q;
        q.push_back(root);
        while (q.size()) {
            int s = q.size();
            for (int i = 0; i < s; i++) {
                auto node = q.front();
                q.pop_front();
                // 找到了叶子节点，直接返回深度
                if (node->left == nullptr && node->right == nullptr) {
                    return depth;
                }
                if (node->left != nullptr)
                    q.push_back(node->left);
                if (node->right != nullptr)
                    q.push_back(node->right);
            }
            depth += 1;
        }
        return depth;
    }
};

752. 打开转盘锁

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有 10 个数字： ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转：例如把 ‘9’ 变为 ‘0’，’0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 ‘0000’ ，一个代表四个拨轮的数字的字符串。列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1 。示例:

1
2
3
4
5
6
输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出：6
解释：
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，
因为当拨动到 "0102" 时这个锁就会被锁定。
  • 寻找最短路径时，同样需要使用 bfs 算法。我们把这个问题看成一个多叉树问题，如果 00 是根节点，那么叶子节点就是 01, 10, 09, 90，同理，也能得到 0000 为根节点时对应的叶子节点
  • 同样，先处理极端情况，如根节点被死锁，以及根节点就是目标的特殊情况
  • 之后，以 0000 为根节点开始 bfs 算法，我们手写两个函数，分别为 _up 和 _down 来对 0000 的每一位进行转动进而得到子节点，如果子节点满足要求，返回此时的深度即可
  • 与二叉树不同的是，二叉树使用 root->left, root->right 能保证不会遍历重复节点，而对于此问题，很有可能从 0000 查找到 5555，又从 5555 查找回 0000，因为只要一直转动下去，0000 也是 5555 的子节点。因此，在遍历期间需要设置一个 map，将遍历过的节点添加进去，保证不会重复遍历一个节点，不走回头路。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
public:

    string _up(string node, int idx) {
        string s = node;
        if (s[idx] == '9')
            s[idx] = '0';
        else
            s[idx] += 1;
        return s;
    }

    string _down(string node, int idx) {
        string s = node;
        if (s[idx] == '0')
            s[idx] = '9';
        else
            s[idx] -= 1;
        return s;
    }

    int openLock(vector<string>& deadends, string target) {
        deque<string> q;
        q.push_back("0000");
        unordered_map<string, int> m;
        for (auto i : deadends)
            m[i] = 10;
        if (m["0000"] == 10)
            return -1;
        int cnt = 1;
        if (target == "0000")
            return 0;
        while (q.size()) {
            int s = q.size();
            for (int i = 0; i < s; i++) {
                auto node = q.front();
                q.pop_front();
                for (int i = 0; i < 4; i++) {
                    string s1 = _up(node, i);
                    if (s1 == target)
                        return cnt;
                    if (m[s1] != 10) {
                        m[s1] = 10;
                        q.push_back(s1);
                    }
                    string s2 = _down(node, i);
                    if (s2 == target)
                        return cnt;
                    if (m[s2] != 10) {
                        m[s2] = 10;
                        q.push_back(s2);
                    }
                }
            }
            cnt += 1;
        }
        return -1;
    }
};
本文相关
感谢上学期间打赏我的朋友们。赛博乞讨：我，秦始皇，打钱。

欢迎订阅我的文章